题目内容
(本题8分)已知二次函数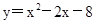 。
。
(1)求函数图象的顶点坐标、对称轴及与坐标轴交点的坐标;
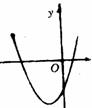
(2)并画出函数的大致图象,并求使y>0的x的取值范围。
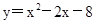 。
。(1)求函数图象的顶点坐标、对称轴及与坐标轴交点的坐标;
(2)并画出函数的大致图象,并求使y>0的x的取值范围。
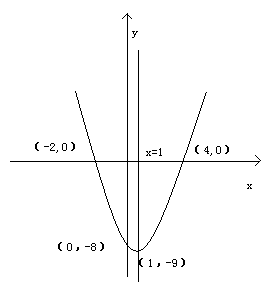
(1)顶点坐标(1,-9),对称轴直线 ,
,
与x轴交点(4,0),(-2,0);与y轴交点标(0,-8)
(2)当 或
或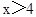 时
时 。
。
 ,
,与x轴交点(4,0),(-2,0);与y轴交点标(0,-8)
(2)当
 或
或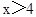 时
时 。
。
试题分析:(1)二次函数
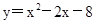 可以化为
可以化为 ,根据式子,顶点坐标为(1,-9),对称轴经过顶点坐标且垂直于x轴,所以对称轴为
,根据式子,顶点坐标为(1,-9),对称轴经过顶点坐标且垂直于x轴,所以对称轴为 ,若
,若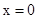 时,
时, ,若
,若 时,
时, 和
和 ,所以与坐标轴的交点为(4,0),(-2,0),(0,-8)
,所以与坐标轴的交点为(4,0),(-2,0),(0,-8)(2)根据(1)中所求得的几个点,可以画出如图所示函数图象,因为函数图象开口向上,所以,要使y>0,由图像可知,函数图像与坐标轴相交时横坐标分别为
 和
和 ,所以,x的取值范围应该是
,所以,x的取值范围应该是 或
或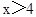 。
。点评:通过一般式转化为顶点式,可以求出函数图象的顶点坐标以及对称轴。函数图像可以直观地看出不同y值对应的x值的取值范围。

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
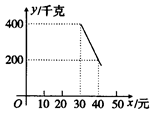
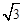 ),且在x轴上截得的线段AB的长为6.
),且在x轴上截得的线段AB的长为6.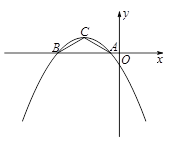
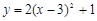 ,可知( )
,可知( )
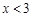 时,y随x的增大而增大
时,y随x的增大而增大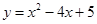 化成
化成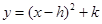 的形式,则
的形式,则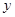 = .
= .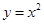 的图象上,若△ABC的面积为2,则这样的C点有
的图象上,若△ABC的面积为2,则这样的C点有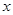 元,每天盈利
元,每天盈利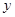 元,则
元,则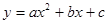 的图象,可知点(b,c)在第 象限.
的图象,可知点(b,c)在第 象限.