题目内容
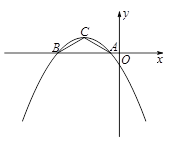
如图,在平面直角坐标系xOy中,二次函数图象的顶点坐标为C(-4,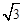 ),且在x轴上截得的线段AB的长为6.
),且在x轴上截得的线段AB的长为6.
(1)求二次函数的解析式;
(2)在y轴上确定一点M,使MA+MC的值最小,求出点M的坐标;
(3)在x轴下方的抛物线上,是否存在点N,使得以N、A、B三点为顶点的三角形与△ABC相似?如果存在,求出点N的坐标;如果不存在,请说明理由.
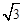 ),且在x轴上截得的线段AB的长为6.
),且在x轴上截得的线段AB的长为6.
(1)求二次函数的解析式;
(2)在y轴上确定一点M,使MA+MC的值最小,求出点M的坐标;
(3)在x轴下方的抛物线上,是否存在点N,使得以N、A、B三点为顶点的三角形与△ABC相似?如果存在,求出点N的坐标;如果不存在,请说明理由.
(1)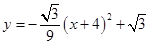 ;(2)(0,
;(2)(0, );(3)(2,
);(3)(2,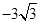 )或(-10,
)或(-10,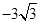 )
)
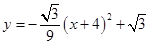 ;(2)(0,
;(2)(0, );(3)(2,
);(3)(2,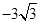 )或(-10,
)或(-10,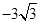 )
)试题分析:(1)先由抛物线的顶点坐标得到抛物线的对称轴,再根据抛物线在x轴上截得的线段AB的长为6,即可得到A、B两点的坐标,从而求得结果;
(2)作点A关于
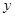 轴的对称点
轴的对称点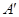 ,可得
,可得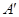 (1,0),连接
(1,0),连接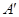 C交
C交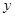 轴于一点即点M,此时MC+MA的值最小,设直线C
轴于一点即点M,此时MC+MA的值最小,设直线C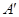 的解析式为
的解析式为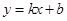 (k≠0),根据待定系数法求得函数关系式,即可得到结果;
(k≠0),根据待定系数法求得函数关系式,即可得到结果;(3)由(1)可知,C(-4,
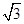 ),设对称轴交x轴于点D,分①AB=AN1=6,②AB=BN2,③N3A=N3B,三种情况讨论即可.
),设对称轴交x轴于点D,分①AB=AN1=6,②AB=BN2,③N3A=N3B,三种情况讨论即可.(1)∵抛物线的顶点坐标为
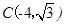 ,
, ∴抛物线的对称轴为直线
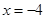 .
.∵抛物线在x轴上截得的线段AB的长为6,
∴A(-1,0),B( -7,0)
设抛物线解析式为

∴
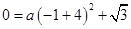
解得
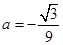
∴二次函数的解析式为
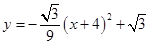 ;
;(2)作点A关于
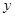 轴的对称点
轴的对称点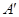 ,可得
,可得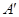 (1,0),连接
(1,0),连接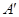 C交
C交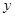 轴于一点即点M,此时MC+MA的值最小
轴于一点即点M,此时MC+MA的值最小
由作法可知,MA=M
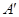
∴MC+MA=MC+M
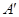 =
=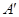 C
C∴当点M在线段
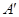 C上时,MA+MC取得最小值
C上时,MA+MC取得最小值∴线段
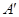 C与
C与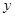 轴的交点即为所求点M
轴的交点即为所求点M设直线C
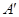 的解析式为
的解析式为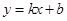 (k≠0)
(k≠0) ∴
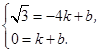
解得
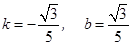
∴直线C
 的解析式为
的解析式为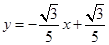
∴点M的坐标为(0,
 );
);(3)由(1)可知,C(-4,
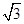 ),设对称轴交x轴于点D
),设对称轴交x轴于点D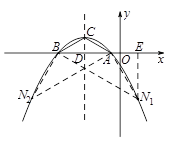
∴AD=3
∴在Rt△ADC中,
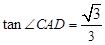
∴∠CAD=30o
∵AC=BC
∴∠ABC=∠CAB=30o
∴∠ACB=120°
①如果AB=AN1=6,过N1作EN1⊥x轴于E
由△ABC∽△BAN1得∠BAN1=120o
则∠EAN1 = 60o
∴N1E=3
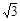 ,AE=3
,AE=3∵A(-1,0)
∴OE=2
∵点N在x轴下方
∴点N2(2,
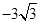 )
)②如果AB=BN2,由对称性可知N2(-10,
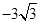 )
)③如果N3A=N3B,那么点N必在线段AB的中垂线即抛物线的对称轴上,在x轴下方的抛物线上不存在这样的点N
经检验,点N1(2,
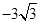 )与N2(-10,
)与N2(-10,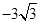 )都在抛物线上
)都在抛物线上综上所述,存在这样的点N,使△NAB∽△ABC,点N的坐标为(2,
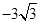 )或(-10,
)或(-10,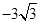 ).
).点评:解答本题的关键是读懂题意,正确画出图形,注意当明确了图象的顶点时,二次函数关系式一半设成顶点式.

练习册系列答案
相关题目
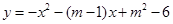 交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.
交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.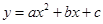 的图象与
的图象与 轴交于点
轴交于点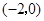 、
、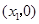 ,且
,且 ,与
,与 轴的正半轴的交点在
轴的正半轴的交点在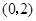 的下方.下列结论:①
的下方.下列结论:①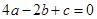 ;②
;② ;③
;③ ;④
;④ .其中正确结论的个数是 个。 ( )
.其中正确结论的个数是 个。 ( )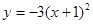 ﹣2,当x 时,函数值y随x的增大而减小.
﹣2,当x 时,函数值y随x的增大而减小. 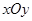 中,将抛物线
中,将抛物线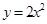 先向左平移1个单位长度,再向下平移3个单位长度后所得到的抛物线的解析式为 ( )
先向左平移1个单位长度,再向下平移3个单位长度后所得到的抛物线的解析式为 ( )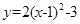

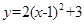
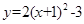
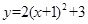
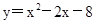 。
。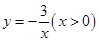 ,②
,②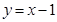 ,③
,③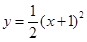 ,④
,④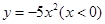 中,
中,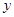 随
随 的增大而增大的函数有( )
的增大而增大的函数有( )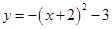 ,下列说法正确的是 ( )
,下列说法正确的是 ( )