题目内容
【题目】在Rt△ABC中,∠ACB=90°,在斜边AB上分别截取AD=AC,BE=BC,DE=6,
点O是△CDE的外心,如图所示,则点O到△ABC的三边的距离之和是 . 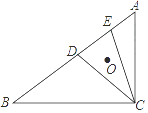
【答案】9
【解析】解:由题意点O是EC、CD垂直平分线的交点,
∵AD=AC,BE=BC,
∴EC的垂直平分线经过B且平分∠B,CD的垂直平分线经过A且平分∠A,
∴O是△ABC的内心,
则r= ![]() (AC+BC﹣AB)=
(AC+BC﹣AB)= ![]() (AD+BE﹣AB)=
(AD+BE﹣AB)= ![]() DE=3,
DE=3,
∴点O到△ABC的三边的距离之和是3r=9,
故答案为9.
根据线段的垂直平分线的判定可知EC的垂直平分线经过B且平分∠B,CD的垂直平分线经过A且平分∠A,根据三角形的内心到三角形三边的距离相等可得O是△ABC的内心,则r= ![]() (AC+BC﹣AB)=
(AC+BC﹣AB)= ![]() (AD+BE﹣AB)=
(AD+BE﹣AB)= ![]() DE,所以点O到△ABC的三边的距离之和是3r。
DE,所以点O到△ABC的三边的距离之和是3r。

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目




