题目内容
【题目】(1)如图 1,在四边形 ABCD 中,AB∥DC,E 是 BC 中点,若 AE 是∠BAD 的平分线,试探究 AB,AD,DC 之间的数量关系,请直接写出结论,无需证明.
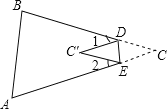
(2)如图 2,在四边形ABCD 中,AB∥DC,AF 与DC 的延长线交于点F,E 是BC 中点,若AE 是∠BAF 的平分线,试探究AB,AF,CF 之间的数量关系,证明你的结论.

【答案】(1)AD=AB+DC;(2)AB=AF+CF,证明详见解析.
【解析】
(1)延长AE交DC的延长线于点F,证明△AEB≌△FEC,根据全等三角形的性质得到AB=FC,根据等腰三角形的判定得到DF=AD,证明结论;
(2)延长AE交DF的延长线于点G,利用同(1)相同的方法证明.
(1)延长AE交DC的延长线于点F.
∵E是BC的中点,∴CE=BE.
∵AB∥DC,∴∠BAE=∠F.
在△AEB和△FEC中,∵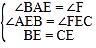 ,∴△AEB≌△FEC,∴AB=FC.
,∴△AEB≌△FEC,∴AB=FC.
∵AE是∠BAD的平分线,∴∠BAE=∠EAD.
∵∠BAE=∠F,∴∠EAD=∠F,∴AD=DF,∴AD=DF=DC+CF=DC+AB;
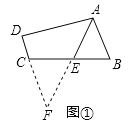
(2)如图②,延长AE交DF的延长线于点G.
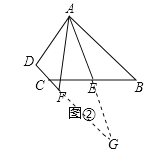
∵E是BC的中点,∴CE=BE.
∵AB∥DC,∴∠BAE=∠G.
在△AEB和△GEC中,∵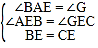 ,∴△AEB≌△GEC,∴AB=GC.
,∴△AEB≌△GEC,∴AB=GC.
∵AE是∠BAF的平分线,∴∠BAG=∠FAG.
∵∠BAE=∠G,∴∠FAG=∠G,∴FA=FG,∴AB=CG=AF+CF.

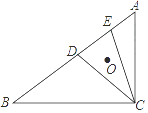
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
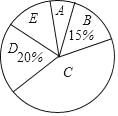
【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组 | 视力 | 人数 |
A | 3.95≤x≤4.25 | 3 |
B | 4.25<x≤4.55 |
|
C | 4.55<x≤4.85 | 18 |
D | 4.85<x≤5.15 | 8 |
E | 5.15<x≤5.45 |
|
根据以上信息,解谷下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人;
(2)本次调查的样本容量是 ,视力在5.15<x≤5.45范围内学生数占被调查学生数的百分比是 %;
(3)在统计图中,C组对应扇形的圆心角度数为 °;
(4)若该校九年级有400名学生,估计视力超过4.85的学生数.