ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§ ΐ÷α’ΐΑκ÷α…œΒΡ![]() Θ§
Θ§![]() ΝΫΒψΖ÷±π±μ Ψ”–άμ ΐ
ΝΫΒψΖ÷±π±μ Ψ”–άμ ΐ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΈΣ‘≠ΒψΘ§»τ
ΈΣ‘≠ΒψΘ§»τ![]() Θ§œΏΕΈ
Θ§œΏΕΈ![]() .
.

Θ®1Θ©![]() ______Θ§
______Θ§![]() ______ΘΜ
______ΘΜ
Θ®2Θ©»τΒψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»œρ
≥ωΖΔΘ§“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»œρ![]() ÷α’ΐΑκ÷α‘ΥΕ·Θ§«σ‘ΥΕ· ±ΦδΈΣΕύ…Ό ±ΘΜΒψ
÷α’ΐΑκ÷α‘ΥΕ·Θ§«σ‘ΥΕ· ±ΦδΈΣΕύ…Ό ±ΘΜΒψ![]() ΒΫΒψ
ΒΫΒψ![]() ΒΡΨύάκ «Βψ
ΒΡΨύάκ «Βψ![]() ΒΫΒψ
ΒΫΒψ![]() ΨύάκΒΡ3±ΕΘΜ
ΨύάκΒΡ3±ΕΘΜ
Θ®3Θ© ΐ÷α…œΜΙ”–“ΜΒψ![]() ±μ ΨΒΡ ΐΈΣ32Θ§»τΒψ
±μ ΨΒΡ ΐΈΣ32Θ§»τΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Ά§ ±¥”Βψ
Ά§ ±¥”Βψ![]() ΚΆΒψ
ΚΆΒψ![]() ≥ωΖΔΘ§Ζ÷±π“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΚΆΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ
≥ωΖΔΘ§Ζ÷±π“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΚΆΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ![]() Βψ‘ΥΕ·Θ§
Βψ‘ΥΕ·Θ§![]() ΒψΒΫ¥ο
ΒψΒΫ¥ο![]() ΒψΚσΘ§‘ΌΝΔΩΧ“‘Ά§―υΒΡΥΌΕ»ΖΒΜΊΘ§‘ΥΕ·ΒΫ÷’Βψ
ΒψΚσΘ§‘ΌΝΔΩΧ“‘Ά§―υΒΡΥΌΕ»ΖΒΜΊΘ§‘ΥΕ·ΒΫ÷’Βψ![]() Θ§«σΒψ
Θ§«σΒψ![]() ΚΆΒψ
ΚΆΒψ![]() ‘ΥΕ·Εύ…ΌΟκ ±Θ§
‘ΥΕ·Εύ…ΌΟκ ±Θ§![]() ΓΔ
ΓΔ![]() ΝΫΒψ÷°ΦδΒΡΨύάκΈΣ4.
ΝΫΒψ÷°ΦδΒΡΨύάκΈΣ4.
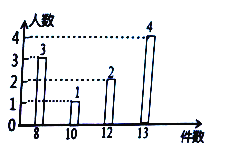
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() ΘΜΘ®2Θ©9Μρ
ΘΜΘ®2Θ©9Μρ![]() ΘΜΘ®3Θ©8Μρ
ΘΜΘ®3Θ©8Μρ![]()
ΓΨΫβΈωΓΩ
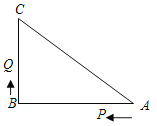
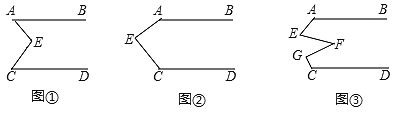
Θ®1Θ©œ»ΗυΨίAΒψ‘Ύ‘≠ΒψΒΡ”“±Ώ“‘ΦΑ|a|=3«σ≥ωaΒΡ÷ΒΘ§‘ΌΗυΨίBΒψ‘Ύ‘≠ΒψΒΡ”“±Ώ“‘ΦΑœΏΕΈOB=5OAΘ§«σ≥ωbΒΡ÷ΒΦ¥Ω…ΘΜ
Θ®2Θ©…η‘ΥΕ· ±ΦδΈΣtΟκΘ§ΗυΨίPA=3PBΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ι–ΈΙΙΫ®ΖΫ≥ΧΘ§Φ¥Ω…ΫβΨωΈ ΧβΘ°
ΫβΘΚΘ®1Θ©ΓΏ ΐ÷α’ΐΑκ÷α…œΒΡAΘ§BΝΫΒψΖ÷±π±μ Ψ”–άμ ΐaΘ§bΘ§|a|=3Θ§œΏΕΈOB=5OAΘ§
Γύa=3Θ§b=15Θ§
Ι ¥πΑΗΈΣΘΚ3Θ§15ΘΜ
Θ®2Θ©…η‘ΥΕ· ±ΦδΈΣtΟκ ±Θ§ΒψPΒΫΒψAΒΡΨύάκ «ΒψPΒΫΒψBΨύάκΒΡ3±ΕΘ°
”…Χβ“βΒΟΘΚAB=15-3=12Θ§
Β±ΒψP‘ΎAΓΔB÷°Φδ ±Θ§”–
2t=3Θ®12-2tΘ©Θ§ΫβΒΟΘΚt=![]() ΘΜ
ΘΜ
Β±ΒψP‘ΎBΒΡ”“±Ώ ±Θ§”–
2t=3Θ®2t-12Θ©Θ§ΫβΒΟt=9ΘΜ
Φ¥‘ΥΕ· ±ΦδΈΣ![]() Μρ9Οκ ±Θ§ΒψPΒΫΒψAΒΡΨύάκ «ΒψPΒΫΒψBΒΡΨύάκΒΡ3±ΕΘΜ
Μρ9Οκ ±Θ§ΒψPΒΫΒψAΒΡΨύάκ «ΒψPΒΫΒψBΒΡΨύάκΒΡ3±ΕΘΜ
Θ®3Θ©ΗυΨίΧβ“βΘ§”…ΒψCΈΣ32Θ§‘ρ
AC=32![]() 3=29Θ§BC=32
3=29Θ§BC=32![]() 15=17Θ§
15=17Θ§
ΓύΒψP‘ΥΕ·ΒΫΒψCΥυ–η“ΣΒΡ ±ΦδΈΣΘΚ![]() ΟκΘ§
ΟκΘ§
ΒψQ‘ΥΕ·ΒΫΒψCΥυ–η“ΣΒΡ ±ΦδΈΣΘΚ![]() ΟκΘ§
ΟκΘ§
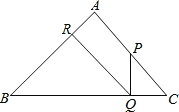
‘ρΩ…Ζ÷ΈΣΝΫ÷÷«ιΩωΫχ––
ΔΌΒ±ΒψPΜΙΟΜ”–ΉΖ…œΒψQ ±Θ§”–ΘΚ
![]() Θ§
Θ§
ΫβΒΟΘΚ![]() ΘΜ
ΘΜ
ΔΎΒ±ΒψP‘ΥΕ·ΒΫΒψCΖΒΜΊ ±Θ§”κΒψQœύ”ωΚσΘ§”κΒψQœύΨύ4Θ§‘ρ”–ΘΚ
![]() Θ§
Θ§
ΫβΒΟΘΚ![]() .
.

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ