题目内容
【题目】哈尔滨实验学校为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买1副围棋和1副中国象棋需用26元;若购买8副围棋和3副中国象棋需用158元;
(1)求每副围棋和每副中国象棋各多少元;
(2)实验中学决定购买围棋和中国象棋共40副,总费用550元,那么实验中学可以购买多少副围棋.
【答案】(1)每副围棋16元,每副中国象棋10元;(2)实验中学可以购买25副围棋.
【解析】
(1)设每副围棋x元,每副中国象棋y元,根据题意得:![]() ,求解即可;
,求解即可;
(2)设购买围棋z副,则购买象棋(40-z)副,根据题意得:16z+10(40-z)≤550,即可求解.
(1)设每副围棋x元,每副中国象棋y元,
根据题意得:![]() ,
,
∴![]() ,
,
∴每副围棋16元,每副中国象棋10元;
(2)设购买围棋z副,则购买象棋(40-z)副,
根据题意得:16z+10(40-z)=550,
∴z=25,
∴实验中学可以购买25副围棋.

【题目】将连续的奇数1,3,5,7,……排成如下表:如图所示,图中的T字框框住了四个数字,若将T字框上下左右移动,按同样的方式可框住另外的四个数.
1 | 3 | 5 | 7 | 9 |
11 | 13 | 15 | 17 | 19 |
21 | 23 | 25 | 27 | 29 |
31 | 33 | 35 | 37 | 39 |
… | … | … | … | … |
(1)设T字框内处于中间且靠上方的数是整个数表当中从小到大排列的第n个数,请你用含n的代数式表示T字框中的四个数的和;
(2)若将T字框上下左右移动,框住的四个数的和能等于2020吗?如能,写出这四个数,如不能,说明理由.
【题目】在一次活动课上,第一小组同学把一个边长为1正方形纸片按如图方法剪裁:第一次剪成四个大小形状一样的小正方形,第二次将其中的一个小正方形再按向样的方法剪成四个小正方形,第三次再按同样的方法将其中一个小正方形剪成四个小正方形,如此循环进行下去.请你替他们完成下列问题:
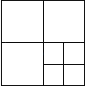
(1)完成表格:
剪的次数 | 1 | 2 | 3 | 4 | 5 | … |
正方形 个数 |
|
| 10 |
|
| … |
(2)如果剪了100次,共剪出 个小正方形;
(3)如果剪了n次,共剪出 个小正方形;
(4)如果剪了n次,则第n次得到的正方形边长是 .