题目内容
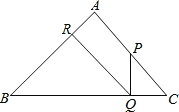
【题目】如图,已知:在△ABC中,∠A=90°,AB=AC=1,P是AC上不与A、C重合的一动点,PQ⊥BC于Q,QR⊥AB于R.
(1)求证:PQ=CQ;
(2)设CP的长为x,QR的长为y,求y与x之间的函数关系式及自变量x的取值范围,并在平面直角坐标系作出函数图象.
(3)PR能否平行于BC?如果能,试求出x的值;若不能,请简述理由.
【答案】(1)证明见解析;(2)y=﹣![]() x+
x+![]() (0<x<1);(3)PR不能平行于BC.
(0<x<1);(3)PR不能平行于BC.
【解析】试题分析:(1)根据题意易得△ABC是等腰直角三角形,则∠B=∠C=45°,然后利用PQ⊥CQ可得到△PCQ为等腰直角三角形,由此得证;
(2)根据等腰直角三角形的性质求出BC=![]() AB=
AB=![]() ,CQ=
,CQ=![]() PC=
PC=![]() x,同理可证得△BQR是等腰直角三角形,则BQ=
x,同理可证得△BQR是等腰直角三角形,则BQ=![]() RQ=
RQ=![]() y,所以可得
y,所以可得![]() y+
y+![]() x=
x=![]() ,变形可求出解析式,然后描点画图即可;
,变形可求出解析式,然后描点画图即可;
(3)由AR=1–y,AP=1–x,则AR=1–(–![]() x+1),当AR=AP时,PR∥BC,所以1–(–
x+1),当AR=AP时,PR∥BC,所以1–(–![]() x+1)=1–x,解得x=
x+1)=1–x,解得x=![]() ,然后利用0<x<1可判断.
,然后利用0<x<1可判断.
试题解析:(1)∵∠A=90°,AB=AC=1,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∵PQ⊥CQ,
∴△PCQ为等腰直角三角形,
∴PQ=CQ;
(2)解:∵△ABC为等腰直角三角形,
∴BC=![]() AB=
AB=![]() ,
,
∵△PCQ为等腰直角三角形,
∴CQ=![]() PC=
PC=![]() x,
x,
同理可证得为△BQR等腰直角三角形,
∴BQ=![]() RQ=
RQ=![]() y,
y,
∵BQ+CQ=BC,
∴![]() y+
y+![]() x=
x=![]() ,
,
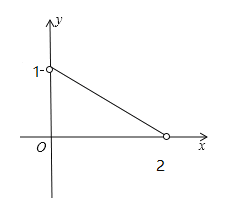
∴y=–![]() x+1(0<x<1),
x+1(0<x<1),
如图,
(3)能.
理由如下:
∵AR=1–y,AP=1–x,
∴AR=1–(–![]() x+1),
x+1),
当AR=AP时,PR∥BC,
即1–(–![]() x+1)=1–x,
x+1)=1–x,
解得x=![]() ,
,
∵0<x<1,∴PR能平行于BC.

练习册系列答案
相关题目