题目内容
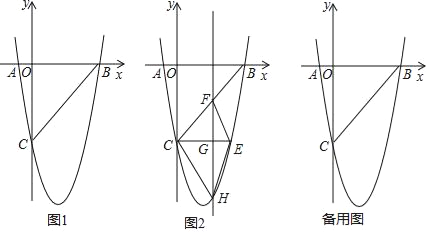
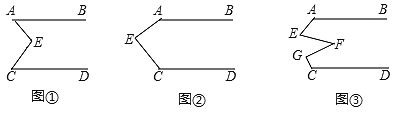
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BAE+∠DCE=∠AEC;
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠BAE+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③,若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG=______°.
【答案】【感知】见解析;【探究】∠BAE+∠AEC+∠DCE=360°;【应用】396°.
【解析】
感知:如图①,过点E作EF∥AB.利用平行线的性质即可解决问题;
探究:如图2中,作EG∥AB,利用平行线的性质即可解决问题;
应用:作FH∥AB,利用平行线的性质即可解决问题;
解:理由如下,
【感知】
过E点作EF//AB
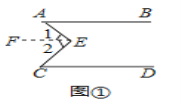
∵AB//CD
∴EF//CD
∵AB//CD
∴∠BAE=∠AEF
∵EF//CD
∴∠CEF=∠DCE
∴∠BAE+∠DCE=∠AEC.
【探究】
过E点作AB//EG.
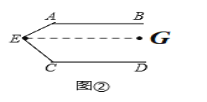
∵AB//CD
∴EG//CD
∵AB//CD
∴∠BAE+∠AEG=180°
∵EG//CD
∴∠CEG+∠DCE=180°
∴∠BAE+∠AEC+∠DCE=360°
【应用】
过点F作FH∥AB.
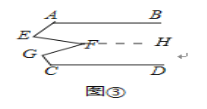
∵AB∥CD,
∴FH∥CD,
∴∠BAE+∠AEF+∠EFH=360°,∠HFG+∠FGC+∠GCD=360°,
∴∠BAE+∠AEF+∠EFH+∠HFG+∠FGC+∠GCD=720°,
∴∠BAE+∠AEF+∠EFH+∠HFG+∠FGC+∠GCD+∠EFG=720°+36°,
∴∠BAE+∠AEF+∠FGC+∠DCG=720°-360°+36°=396°
故答案为:396°.

【题目】在一次活动课上,第一小组同学把一个边长为1正方形纸片按如图方法剪裁:第一次剪成四个大小形状一样的小正方形,第二次将其中的一个小正方形再按向样的方法剪成四个小正方形,第三次再按同样的方法将其中一个小正方形剪成四个小正方形,如此循环进行下去.请你替他们完成下列问题:
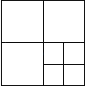
(1)完成表格:
剪的次数 | 1 | 2 | 3 | 4 | 5 | … |
正方形 个数 |
|
| 10 |
|
| … |
(2)如果剪了100次,共剪出 个小正方形;
(3)如果剪了n次,共剪出 个小正方形;
(4)如果剪了n次,则第n次得到的正方形边长是 .