��Ŀ����
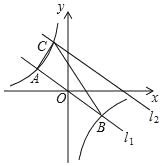
����Ŀ����ͼ,��֪������y=ax![]() +bx+c����A(-3,0),B(1,0),C(0,3)����,�䶥��ΪD,�Գ�����ֱ��l,l��x�ύ�ڵ�H
+bx+c����A(-3,0),B(1,0),C(0,3)����,�䶥��ΪD,�Գ�����ֱ��l,l��x�ύ�ڵ�H
(1)��������ߵĽ���ʽ;
(2)����P�Ǹ������߶Գ���l�ϵ�һ������,���PBC�ܳ�����Сֵ;
(3)��ͼ(2),��B���߶�AD�ϵ�һ������(E��A.D���غ�),��E����ƽ����y���ֱ�߽��������ڵ�F,��x���ڵ�G,���E�ĺ�����Ϊm,��ADF�����ΪS.
����S��m�ĺ�����ϵʽ
��S�Ƿ�������ֵ?������,������ֵ����ʱ��E������;��������,��˵�����ɡ�
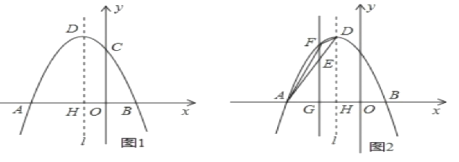
���𰸡���1��y=-x![]() -2x+3;��2��3
-2x+3;��2��3![]() +
+![]()
��3����![]() �ڣ�-2,2��
�ڣ�-2,2��
��������
(1)���ݺ���ͼ��������,�ô���ϵ����ȷ�����κ����Ľ���ʽ����;
(2)����BC�Ƕ�ֵ,�õ���PB+PC��Сʱ,��PBC���ܳ���С,���ݵ�����������Ӧ�߶εij�����;
(3)���E�ĺ�����Ϊm,��ʾ��E(m,2m+6),F(m,-m![]() -2m+3),����ʾ��EF�ij�,�Ӷ���ʾ
-2m+3),����ʾ��EF�ij�,�Ӷ���ʾ
��S��m�ĺ�����ϵ,Ȼ������κ�������ֵ���ɽ��
(1)�������֪

���: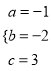
�������ߵĽ���ʽΪ:y=-x![]() -2x+3;
-2x+3;
��2������PBC���ܳ�Ϊ:PB+PC+BC
��BC�Ƕ�ֵ,
�൱PB+PC��Сʱ,��PBC���ܳ���С
�ߵ�A��B���ڶԳ���Գ�,

������AC��1�ڵ�P,����PΪ����ĵ�
.��AP= BP
����PBC���ܳ���С��:
PB+PC+BC=AC+BC
��A(-3,0),B(1,0),C(0,3),
��AC=3![]() BC=
BC=![]()
����PBC�ܳ�����СֵΪ3![]() +
+![]()
��3����:������y=-x![]() -2x+3;����D������Ϊ(-1,4)
-2x+3;����D������Ϊ(-1,4)
��A(-3,0)
��ֱ��AD�Ľ���ʽΪy=2x+6
�ߵ�E�ĺ�����Ϊm
��E(m,2m+6),F(m,-m![]() -2m+3
-2m+3
��EF=-m![]() -2m+3-(2m+6)=-m
-2m+3-(2m+6)=-m![]() -4m-3
-4m-3
��S= S��DEF+S��AEF=![]()
��![]()
�൱m=-2ʱ��S������ֵΪ1
��ʱ��E������Ϊ��-2,2��

 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�����Ŀ����������ϣ�����ʦ��ʾ����ͼһ������������ͬѧ�ǵ�һ�����飬��������ĸ��۵㣺
A���������ң��˴����أ� B���������棬�˴�ƽ�⣻
C�������Ը˴˳ɾͣ� D����������������˫Ӯ��
Ҫ��ÿ��ѡȡ����һ���۵�д���Լ��ĸ�����ͬѧ�ǵ�ѡ�������С����������ͼ������������ͼ���������ͼ�����ṩ����Ϣ������������⣺
�۵� | Ƶ�� | Ƶ�� |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |

��1���μӱ������۵�ѧ�������� ���ˣ�
��2������a���� ����b���� ����
��3��������ͳ��ͼ����������
��4��������A��B��C��D�ĸ��۵�����ѡ������Ϊ�ݽ����⣬�����б�����״ͼ�ķ�����ѡ�й۵�D����������������˫Ӯ���ĸ��ʣ�