题目内容
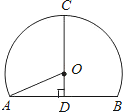
如图，在⊙O内有折线OABC，点B、C在圆上，点A在⊙O内，其中OA=4cm，BC=10cm，∠A=∠B=60°，则AB的长为（ ）
| A．5cm | B．6cm | C．7cm | D．8cm |
延长AO交BC于D，作OE⊥BC于E，
设AB的长为xcm，
∵∠A=∠B=60°，∴∠ADB=60°；
∴△ADB为等边三角形；
∴BD=AD=AB=x；
∵OA=4cm，BC=10cm，
∴BE=5cm，DE=（x-5）cm，OD=（x-4）cm，
又∵∠ADB=60°，
∴DE=
OD，
∴x-5=
（x-4），
解得：x=6．
故选B．
设AB的长为xcm，
∵∠A=∠B=60°，∴∠ADB=60°；
∴△ADB为等边三角形；
∴BD=AD=AB=x；
∵OA=4cm，BC=10cm，
∴BE=5cm，DE=（x-5）cm，OD=（x-4）cm，
又∵∠ADB=60°，
∴DE=
| 1 |
| 2 |
∴x-5=
| 1 |
| 2 |
解得：x=6．
故选B．
练习册系列答案
相关题目
CO交⊙O于点D，连接AD．