题目内容
如图6,在△ABC中,AB=4,AC=10,⊙B与⊙C是两个半径相等的圆,且两圆相切,如果点A在⊙B内,那么⊙B的半径r的取值范围是_______________.
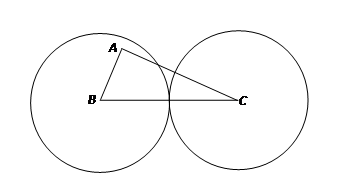
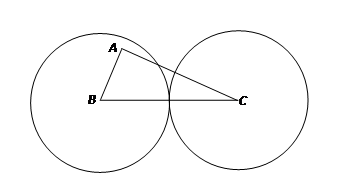
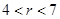
根据三角形三边关系可得,|AB-AC|<BC<AB+BC,代入数据即可得出6<2r<14,即有3<r<7.以及AB=4,即r>4;综上所述,即可得出r的取值范围.
解:根据题意可得,当A、B、C三点构成一个三角形时,
利用三角形三边之间的关系,
|AB-AC|<BC<AB+BC,
即有3<r<7.
又∵A在⊙B内,且AB=4,即r>4;
综上可得,4<r<7.
故答案为:4<r<7.
本题主要考查了三角形三边之间的关系和相切两圆的性质,属于基础练习性题目,希望学生在学习的过程中多加总结归纳,找出适合自己的学习方法.
解:根据题意可得,当A、B、C三点构成一个三角形时,
利用三角形三边之间的关系,
|AB-AC|<BC<AB+BC,
即有3<r<7.
又∵A在⊙B内,且AB=4,即r>4;
综上可得,4<r<7.
故答案为:4<r<7.
本题主要考查了三角形三边之间的关系和相切两圆的性质,属于基础练习性题目,希望学生在学习的过程中多加总结归纳,找出适合自己的学习方法.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为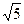 ,过点C作⊙A的切线交
,过点C作⊙A的切线交 轴于点B(-4,0)
轴于点B(-4,0) .
.

 ,DF
,DF ,试建立
,试建立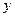 关于
关于 的函数关系式,
的函数关系式,




 ).
).