题目内容
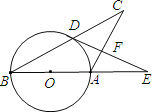
【题目】如图，将△ABC绕顶点C逆时针旋转得到△A′B′C，且点B刚好落在A′B′上．若∠A＝25°，∠BCA′＝45°，则∠A′BA＝___________度
【答案】40
【解析】
由旋转的性质可得：∠A′=∠A=25°，∠B′=∠ABC，CB=C B′，根据等边对等角可得：∠B′=∠B′BC，根据三角形外角的性质可得：∠B′BC=∠BCA′＋∠A′=70°，从而求出∠B′BC和∠ABC，即可求出∠A′BA.
解：由旋转的性质可得：∠A′=∠A=25°，∠B′=∠ABC，CB=C B′
∴∠B′=∠B′BC
∵∠BCA′＝45°，
∴∠B′BC=∠BCA′＋∠A′=70°
∴∠ABC=∠B′=∠B′BC=70°
∴∠A′BA=180°－∠B′BC－∠ABC=40°
故答案为：40
练习册系列答案
相关题目
【题目】我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量y（万件）与月份x（月）的关系为：
，每件产品的利润z（元）与月份x（月）的关系如下表：
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
z | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
（1）请你根据表格求出每件产品利润z（元）与月份x（月）的关系式；
（2）若月利润w（万元）=当月销售量y（万件）×当月每件产品的利润z（元），求月利润w（万元）与月份x（月）的关系式；
（3）当x为何值时，月利润w有最大值，最大值为多少？
【题目】二次函数
（
，
，
为常数且
）中的
与
的部分对应值如下表：
| －1 | 0 | 1 | 3 |
| －1 | 3 | 5 | 3 |
给出了结论：
（1）二次函数有最大值，最大值为5；（2）
；（3）
时，的值随值的增大而减小；（4）3是方程
的一个根；（5）当
时，
.则其中正确结论的个数是（ ）
A.4B.3C.2D.1
