题目内容
【题目】平面直角坐标系中,直线![]() 与x轴、y轴分别胶于A、C两点,直线
与x轴、y轴分别胶于A、C两点,直线![]() 与x轴、y轴分别交于B、D两点.
与x轴、y轴分别交于B、D两点.
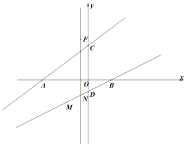
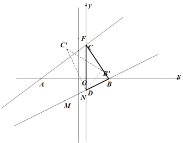
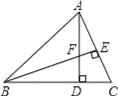
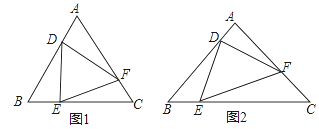
(1)如图1,点F是直线![]() 上的动点,当
上的动点,当![]() 的面积等于
的面积等于![]() 时,有一线段
时,有一线段![]() (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF的周长最小时点N的横坐标.
(点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF的周长最小时点N的横坐标.
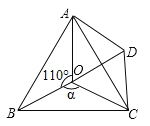
(2)如图2,将![]() 绕点D逆时针旋转
绕点D逆时针旋转![]() ,记旋转中的
,记旋转中的![]() 为
为![]() ,若直线
,若直线![]() 与直线AC交于点P,直线
与直线AC交于点P,直线![]() 与直线DC交于点Q,当
与直线DC交于点Q,当![]() 是等腰三角形时,直接写出CP的值.
是等腰三角形时,直接写出CP的值.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)作点A关于直线BD的对称点![]() ,把
,把![]() 沿平行直线BD方向平移到
沿平行直线BD方向平移到![]() ,且
,且![]() ,连接
,连接![]() ,交直线BD于点N,把点N沿直线BD向左平移
,交直线BD于点N,把点N沿直线BD向左平移![]() 得点M,求出直线
得点M,求出直线![]() 的解析式和直线BD解析式,算出交点横坐标,即为四边形AMNF的周长最小时点N的横坐标;
的解析式和直线BD解析式,算出交点横坐标,即为四边形AMNF的周长最小时点N的横坐标;
(2)先根据等面积法求出DH的长,算出![]() 的值,再分①当
的值,再分①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,④当
时,④当![]() 时,分别求出PC的值即可.
时,分别求出PC的值即可.
(1)作点A关于直线BD的对称点![]() ,把
,把![]() 沿平行直线BD方向平移到
沿平行直线BD方向平移到![]() ,且
,且![]() ,连接
,连接![]() ,交直线BD于点N,把点N沿直线BD向左平移
,交直线BD于点N,把点N沿直线BD向左平移![]() 得点M,
得点M,
此时四边形AMNF的周长最小,理由如下:
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
过![]() 作
作![]() ,
,

∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 的解析式为
的解析式为![]() ①,
①,
∵![]() ,
,![]() ,
,
∴直线BD解析式为![]() ②,
②,
联立①②得,![]() ,
,
∴N点的横坐标为:![]() ;
;
(2)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
BC边上的高为DH,
根据等面积法得,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
①当![]() 时,如图,
时,如图,
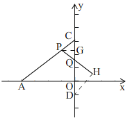
过点P作![]() ,过点D作
,过点D作![]() ,
,
∵![]() ,
,
∴设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴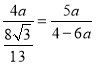 ,
,
∴![]() ,∴
,∴![]() ;
;
②当![]() 时,如图,
时,如图,
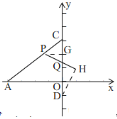
过点P作![]() ,过H作
,过H作![]() ,
,
∵![]() ,
,
∴设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
当![]() ,
,
用①的方法得出,![]() ,
,
当△QPG∽△QDH,
同①方法得出![]() ;
;
③当![]() 时,如图,
时,如图,
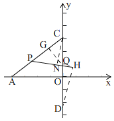
过点Q作![]() ,过点C作
,过点C作![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
利用等面积法得,![]() ,
,
∴![]()
∴△CQN∽△DOH,
用①的方法得出![]()
综上所述,PC的值为![]() ;
;![]() ;
;![]() ;
;![]() .
.

【题目】万州三中初中数学组深知人生最具好奇心和幻想力、创造力的时期是中学时代,经研究,为我校每一个初中生推荐一本中学生素质数育必读书《数学的奥秘》,这本书就是专门为好奇的中学生准备的.这本书不但给于我们知识,解答生活中的疑惑,更重要的是培养我们细致观察、认真思考、勤于动手的能力.经过一学期的阅读和学习,为了了解学生阅读效果,我们从初一、初二的学生中随机各选20名,对《数学的奥秘》此书阅读效果做测试(此次测试满分:100分).通过测试,我们收集到20名学生得分的数据如下:
初一 | 96 | 100 | 89 | 95 | 62 | 75 | 93 | 86 | 86 | 93 |
95 | 95 | 88 | 94 | 95 | 68 | 92 | 80 | 78 | 90 | |
初二 | 100 | 98 | 96 | 95 | 94 | 92 | 92 | 92 | 92 | 92 |
86 | 84 | 83 | 82 | 78 | 78 | 74 | 64 | 60 | 92 |
通过整理,两组数据的平均数、中位数、众数和方差如表:
年级 | 平均数 | 中位数 | 众数 | 方差 |
初一 | 87.5 | 91 | m | 96.15 |
初二 | 86.2 | n | 92 | 113.06 |
某同学将初一学生得分按分数段(![]() ,
,![]() ,
,![]() ,
,![]() ),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如图(均不完整),初一学生得分频数分布直方图 初二学生得分扇形统计图(注:x表示学生分数)
),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如图(均不完整),初一学生得分频数分布直方图 初二学生得分扇形统计图(注:x表示学生分数)
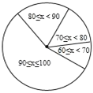
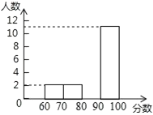
请完成下列问题:
(1)初一学生得分的众数![]() ________;初二学生得分的中位数
________;初二学生得分的中位数![]() ________;
________;
(2)补全频数分布直方图;扇形统计图中,![]() 所对用的圆心角为________度;
所对用的圆心角为________度;
(3)经过分析________学生得分相对稳定(填“初一”或“初二”);
(4)你认为哪个年级阅读效果更好,请说明理由.