题目内容
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数且
为常数且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 1 | 3 |
| -1 | 3 | 5 | 3 |
给出了结论:
(1)二次函数![]() 有最大值,最大值为5;(2)
有最大值,最大值为5;(2)![]() ;(3)
;(3)![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;(4)3是方程
值的增大而减小;(4)3是方程![]() 的一个根;(5)当
的一个根;(5)当![]() 时,
时,![]() .则其中正确结论的个数是( )
.则其中正确结论的个数是( )
A.4B.3C.2D.1
【答案】B
【解析】
当x=0时,y=3,则c=3;当x=-1时,y=-1;当x=1时,y=5,代入即可求函数解析式y=-x2+3x+3;进而可以进行判断.
解:∵![]() 时
时![]() ,
,![]() 时
时![]() ,
,![]() 时
时![]() .
.
∴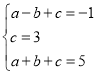 ,
,
解得: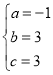 .
.
∴ .
.
当![]() 时,
时,![]() 有最大值,为
有最大值,为![]() ,①错误.
,①错误.
![]() ,②正确.
,②正确.
∵a=-1<0,开口对称轴为直线![]() ,所以,当
,所以,当![]() 时,
时,![]() 随
随![]() 的增大而减小,③错误.
的增大而减小,③错误.
方程为![]() ,解得
,解得![]() ,
,![]() ,所以3是方程
,所以3是方程
![]() 的一个根,④正确.
的一个根,④正确.
∵![]() 时,
时,![]() .
.
∴![]() 时,
时,![]() .
.
∵![]() 时,
时,![]() ,且函数有最大值.
,且函数有最大值.
∴当![]() 时,
时,![]() ,⑤正确.
,⑤正确.
综上,正确的有②④⑤,共3个,故选B.

练习册系列答案
相关题目
【题目】某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价y1(单位:元)与它的边长x(单位:cm)满足关系式y1=![]() ,每张薄板的出厂价y2(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据.
,每张薄板的出厂价y2(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据.
薄板的边长(cm) | 20 | 30 |
出厂价(元/张) | 50 | 70 |
(1)求一张薄板的出厂价y2与边长x之间满足的函数关系式;
(2)已知:利润=出厂价﹣成本价
①求一张薄板的利润y与边长x之间满足的函数关系式;
②当边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?