题目内容
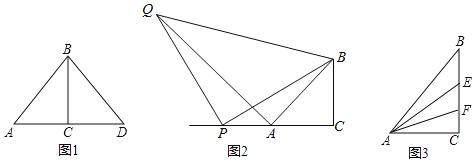
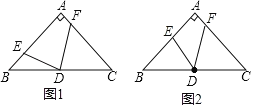
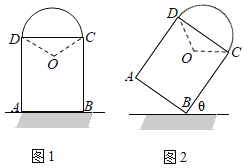
【题目】图1为一艺术拱门，下部为矩形ABCD，AB、AD的长分别为
m和4m，上部是圆心为O的劣弧CD，∠COD＝120°．现欲以点B为支点将拱门放倒，放倒过程中矩形ABCD所在的平面始终与地面垂直，如图2所示．设BC与地面水平线所成的角为
，记拱门上的点到地面的距离为h，当h取最大值时，此时为________°．
【答案】60°
【解析】
在门放倒的过程中，最高点弧CD上时，h的高度等于扇形半径加上点O到底面的距离，继续移动最高点不在弧CD上时，点到底面的距离就是D到底面的距离，即D就是最高点．显然最高点在弧CD上时的高度要大于最高点在D点上时，只有当OB垂直底面时候，O到底面有最大值，即h为最大，也就是图1中OB移动到BC时的角度就是门旋转的角度，
，利用三角函数算出
即可．
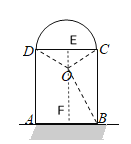
解：如图连接OB，
过O点向AB做垂线交DC于E点，AB于F点．
当OB垂直底面时h有最大值；
∵∠DOC=
∴∠EOC=
由三角函数
OC×sin =EC
∵DC=2
∴EC=
∴OC=
=2
∴OE=1
则OF=3
∵tan
=
∴∠BOF=
∵OF∥BC
∴∠OBC=
当OB旋转到BC处时候，h有最大值，
此时BC也旋转了
则
故本题答案为．
. 
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
