Question

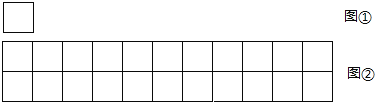
【题目】现有若干根长度相同的火柴棒，用a根火柴棒，按如图①摆放时可摆成m个正方形，用b根火柴棒，按如图②摆放时可摆成2n个正方形．(m、n是正整数)

（1）如图①，当m=4时，a=______；如图②，当b=52时，n=______；

（2）当若干根长度相同的火柴棒，既可以摆成图①的形状，也可以摆成图②的形状时，m与n之间有何数量关系，请你写出来并说明理由；

（3）现有61根火柴棒，用若干根火柴棒摆成图①的形状后，剩下的火柴棒刚好可以摆成图②的形状．请你直接写出一种摆放方法．

Answer 1

【答案】（1）a=13，n=10；（2）3m+1=5n+2；（3）如图①摆放1个正方形，如图②摆放11个正方形

【解析】

（1）根据每多一个正方形多用2根火柴棒写出摆放m个正方形所用的火柴棒的根数，然后把m=4代入进行计算即可得解；

（2）根据a相等列出关于m、n的关系式；

（3）可以摆出图①说明a是比3的倍数多1的数，可以摆出图②说明2a是比5的倍数多2的数，所以，2a取5与6的倍数大2的数，并且现有61根火柴棒进而得出答案．

（1）由图可知，图①每多1个正方形，多用3根火柴棒，所以，m个小正方形共用3m+1根火柴棒，

图②每多2个正方形，多用5根火柴棒，所以，2n个小正方形共用5n+2根火柴棒，

当m=4时，a=3×4+1=13，

图②可以摆放5n+2=52个小正方形,

∴n=10.（2）∵都用a根火柴棒，

∴3m+1=5n+2，

整理得，3m=5n+1；

（3）∵3m+1+5n+2=61，

∴3m+5n=58，

当m=1，n=11，是方程的根，

∴第一个图形摆放3×1+1=4根火柴棒，

第二个图形摆放5×11+2=57根火柴棒，

如图，

∵4+57=61，

∴符合题意（答案不唯一）．