题目内容
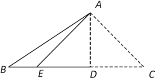
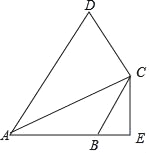
【题目】如图,在四边形ABCD中,AC平分∠DAB,∠D+∠ABC=180°,CE⊥AB,垂足为E,若△ACD和△ABC的面积分别为50和38,则△CBE的面积为_____.
【答案】6
【解析】
过C作CF⊥AD于F,先判定△CDF≌△CBE(AAS),即可得出S△CDF=S△CBE,设S△CDF=S△CBE=x,再根据Rt△ACF≌Rt△ACE(HL),即可得出S△ACF=S△ACE,最后解方程即可得到△CBE的面积.
如图,过C作CF⊥AD于F,则∠CFD=∠E=90°,
∵∠D+∠ABC=180°,∠CBE+∠ABC=180°,
∴∠D=∠CBE,
∵AC平分∠DAE,CF⊥AD,CE⊥AE,
∴CF=CE,
∴△CDF≌△CBE(AAS),
∴S△CDF=S△CBE,
设S△CDF=S△CBE=x,
又∵∠AFC=∠E=90°,AC=AC,
∴Rt△ACF≌Rt△ACE(HL),
∴S△ACF=S△ACE,
又∵△ACD和△ABC的面积分别为50和38,
∴50﹣x=38+x,
解得x=6,
故答案为:6.

练习册系列答案
相关题目