题目内容
【题目】如图,在Rt△ACB中,四边形DECF为正方形,回答下列问题.
(1)简述图1经过怎样的变换可形成图2?
(2)若AD=3,BD=4,求△ADE与△BDF的面积之和.
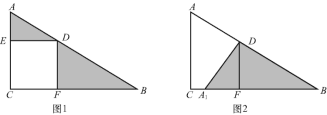
【答案】(1)把△ADE绕D点逆时针旋转90°得△A1DF;(2)6.
【解析】
(1)观察图形,发现DA旋转到DA1,DE旋转到DF,而∠EDF=90°,由旋转的定义即可描述由图(1)变成图(2)的形成过程;
(2)由图形的旋转可知,图形顺时针旋转了90°,即∠EDF=∠ADA1=90°,可得∠A1DB=90°,△ADE和△BDF面积的和即为△A1DB的面积.
(1)由题意可得,把△ADE绕D点逆时针旋转90°得△A1DF.
(2)由图及(1)知S△ADE+S△BDF=![]() ,
,
根据图形的旋转性质可知AD=A1D,∠ADE=∠A1DF,
又∵∠ADE+∠FDB=90°,
∴∠A1DF+∠FDB=90°,即∠A1DB=90°.
∴在Rt△A1DB中,A1D=AD=3,BD=4,
![]() A1D×BD=6,
A1D×BD=6,
∴△ADE与△BDF面积之和为6.

练习册系列答案
相关题目
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?