题目内容
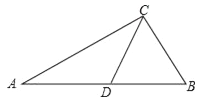
【题目】如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=![]() ,tanA=
,tanA=![]() ,BC=2
,BC=2![]() ,求边AB的长和cos∠CDB的值.
,求边AB的长和cos∠CDB的值.
【答案】边AB的长为6,cos∠CDB=![]()
【解析】整体分析:
过点C作CE⊥AB于点E,解Rt△BCE,求CE,BE,在Rt△ACE中,由CE,tanA的值求AE,则可求AB;在Rt△CDE中,求出DE,CD,由余弦的定义求cos∠CDB.
解:过点C作CE⊥AB于点E,
在Rt△BCE中,∵BC=![]() ,sinB=
,sinB=![]() ,
,
∴CE=BC·sinB=![]() ×
×![]() =2,∴BE=
=2,∴BE=![]() =
=![]() =2,
=2,
在Rt△ACE中,∵tanA=![]() ,
,
∴AE=![]() =
=![]() =4,∴AB=AE+BE=4+2=6,
=4,∴AB=AE+BE=4+2=6,
∵CD是边AB上的中线,∴BD=![]() AB=3,∴DE=BD﹣BE=1,
AB=3,∴DE=BD﹣BE=1,
在Rt△CDE中,∵CD=![]() =
=![]() =
=![]() ,
,
∴cos∠CDB=![]() =
=![]() =
=![]() .
.
故边AB的长为6,cos∠CDB=![]() .
.


练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目