题目内容

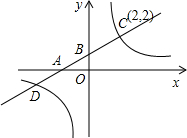
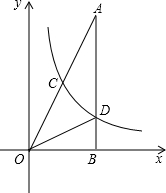
如图，在Rt△AOB中，∠ABO=90°，OB=4，AB=8，且反比例函数y=
k
x
在第一象限内的图象分别交OA、AB于点C和点D，连结OD，若S△BOD=4，
（1）求反比例函数解析式；
（2）求C点坐标．
（1）∵S△BOD=
1
2
k，
∴
1
2
k=4，解得k=8，
∴反比例函数解析式为y=
8
x
；

（2）设直线OA的解析式为y=ax，把A（4，8）代入得4a=8，解得a=2，
所以直线OA的解析式为y=2x，
解方程组
y=2x
y=
8
x
得
x=2
y=4
或
x=-2
y=-4
，
所以C点坐标为（2，4）．
练习册系列答案
相关题目
如图所示，直线l1的方程为y=-x+1，直线l2的方程为y=x+5，且两直线相交于点P，过点P的双曲线y=
k
x
与直线l1的另一交点为Q（3，m）．
（1）求双曲线的解析式．
（2）根据图象直接写出不等式
k
x
＞-x+1的解集．
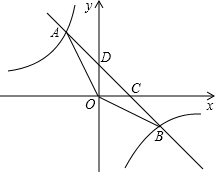已知一次函数与反比例函数的图象交于A（-2，4）、B（4，-2）两点，一次函数与x轴、y轴交于C、D两点，如图所示．
（1）求一次函数与反比例函数的表达式；
（2）求△AOB的面积．
如图，一次函数y=kx+b的图象与反比例函数y=
m
x
的图象相交于点C（2，2），与x轴负半轴交于点A，与y轴交于点B，O为坐标原点，且tan∠BAO=
2
3
．
（1）求反比例函数与一次函数的表达式．
（2）求一次函数与反比例函数图象的另一交点D的坐标．
已知直线y1=-2x+2上有两点A（2，-2），B（-1，4）．
（1）请说明存在一个反比例函数y2=
k
x
，它的图象同时经过点A、B，并求出这个函数的解析式；
（2）用描点法在右图中画出该反比例函数的图象，并根据图象判断，当x取何值时，y1＞y2．
如图，正比例函数y1=k1x与反比例函数y2=
k2
x
相交于A、B点．已知点A的坐标为A（4，n），BD⊥x轴于点D，且S△BDO=4．过点A的一次函数y3=k3x+b与反比例函数的图象交于另一点C，与x轴交于点E（5，0）．
（1）求正比例函数y1、反比例函数y2和一次函数y3的解析式；
（2）结合图象，求出当k3x+b＞
k2
x
＞k1x时x的取值范围．
如图，已知一次函数y1=kx+b的图象与反比例函数y2=-
8
x
的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是-2．
求：（1）一次函数的解析式；
（2）△AOB的面积；
（3）并利用图象指出，当x为何值时有y1＞y2；当x为何值时有y1＜y2．
已知正比例函数y=x和反比例函数y=
1
x
的图象（如图），请你画出函数y=x-
1
x
的大致图象，并用文字说明所画图象的特征．
已知，A、B、C、D、E是反比例函数y=
16
x
（x＞0）图象上五个整数点（横、纵坐标均为整数），分别以这些点向横轴或纵轴作垂线段，由垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图所示的五个橄榄形（阴影部分），则这五个橄榄形的面积总和是______（用含π的代数式表示）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网