题目内容
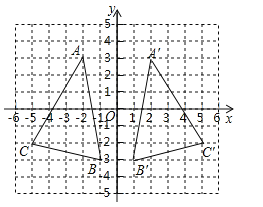
【题目】已知![]() 在平面直角坐标系中的位置如图所示,且三个顶点都在正方形网格的格点上.
在平面直角坐标系中的位置如图所示,且三个顶点都在正方形网格的格点上.
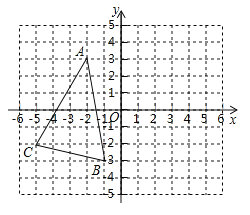
(1)把![]() 沿
沿![]() 轴翻折得到
轴翻折得到![]() ,画出
,画出![]() ,并写出点
,并写出点![]() 的坐标_____;
的坐标_____;
(2)若点![]() 在
在![]() 内部,当
内部,当![]() 沿
沿![]() 轴翻折后,点
轴翻折后,点![]() 对应点
对应点![]() 的坐标是_____;
的坐标是_____;
(3)求![]() 的面积.
的面积.
【答案】(1)如图见解析;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的面积
的面积![]() .
.
【解析】
(1)根据网格特点得出A、B、C三点的对应点A′、B′、C′,顺次连接即可得△A′B′C′;根据关于y轴对称的点的坐标特征:纵坐标不变,横坐标互为相反数即可得A′坐标;
(2)根据关于y轴对称的点的坐标特征:纵坐标不变,横坐标互为相反数即可得答案;
(3)利用网格特点及勾股定理,用△ABC所在矩形的面积减去三个三角形的面积即可得答案.
(1)如图,△A′B′C′即为所求,
∵点A坐标为(-2,3),
∴点A关于y轴的对称点A′坐标为(2,3),
故答案为:(2,3)
(2)∵点P(m,n),
∴点![]() 关于y轴的对称点
关于y轴的对称点![]() 的坐标是(-m,n),
的坐标是(-m,n),
故答案为:(-m,n)
(3)∵A(-2,3),B(-1,-3),C(-5,-2),
∴△ABC的面积![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目