题目内容
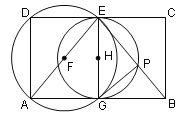
【题目】如图,矩形ABCD的面积为15,边AB比AD大2,E为CD中点,以AE为直径的⊙F交AB于G点,以EG为直径的⊙H交EB于P点,回答下列问题:
(1)求AB、AD的长;
(2)求证:PG为⊙F的切线;
(3)求PG的长.
【答案】(1)AD=3,AB=5;(2)证明见解析;(3)PG=![]() .
.
【解析】
(1)根据矩形ABCD的面积和边AB比AD大2,列方程可求出;
(2)连接FG,通过中位线定理说明FG∥EB,再利用圆周角定理说明PG⊥EB,即可证明PG⊥FG;
(3)根据(1)(2)可得EG、BG的长,再求出BE的长,在直角△EBG中利用面积公式可得:BE×PG=EG×BG,即可解出PG.
解:(1)设AD=![]() ,则AB=
,则AB=![]() +2,
+2,
∴![]() .
.
解得![]() =-5(舍去),
=-5(舍去),![]() =3.
=3.
∴AD=3,AB=5.
(2)连接FG,
∵AE是⊙F的直径,且点G在⊙F上,
∴EG⊥AB.
又∵E为CD的中点,
∴G为AB的中点.
又∵F为AE的中点,
∴FG∥EB.
又∵EG是⊙H的直径,且点P在⊙H上,
∴PG⊥EB.
∴PG⊥FG.
又∵点G在⊙F上,
∴PG是⊙F的切线.
(3)由(1)(2)可知GE=AD=3,GB=![]() AB=
AB=![]() ,GE⊥GB,PG⊥EB,
,GE⊥GB,PG⊥EB,
∴EB=![]() =
=![]() .
.
∴由Rt△BGE的面积公式可得PG![]() =
=![]() .
.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目