��Ŀ����
����Ŀ�����Ǹ������¶��壺��һ�������ڽ���ȵ��ı��ν������ڽ��ı��Σ������������⣺
��1��д��һ������ѧ���������ı������ǵ��ڽ��ı��ε�ͼ�ε����ƣ�
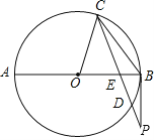
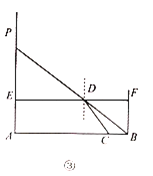
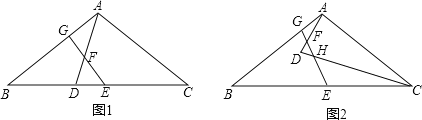
��2����ͼ1���ڡ�ABC�У�AB��AC����D��BC�ϣ���CD��CA����E��F�ֱ�ΪBC��AD���е㣬����EF���ӳ���AB�ڵ�G����֤���ı���AGEC�ǵ��ڽ��ı��Σ�
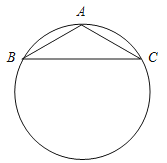
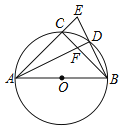
��3����ͼ2������D�ڡ�ABC���ڲ�����2���е������������䣬EF��CD���ڵ�H��ͼ���Ƿ���ڵ��ڽ��ı��Σ������ڣ�ָ�����ĸ��ı��Σ���֤�����������ڣ���˵�����ɣ�
���𰸡���1���������Σ�����Σ��������Σ�����2������������3�����ڵ��ڽ��ı��Σ�Ϊ�ı���AGHC��֤����������
��������
��1���ڽ���ȵ��ı����кܶ࣬���Ρ������λ��ߵ������ζ�������һ���ڽ���ȣ�
��2���Ȿ�������ַ�������������λ�ߵ����ʣ��ҳ���Ӧ��ȵĽǣ����ô���ϵ���������x��д������x�Ĵ���ʽ�������ҳ���Ӧ��ȵĽǣ�
��3������������֪�����������ı��μ�Ϊ�ڶ�����ı��Σ�
��1�����������������������
��2��֤��һ��ȡAC���е�M������ME��MF

�ߵ�EΪBC�е㣬
��EMΪ��ABC����λ�ߣ�
��EM��AB����EM��![]() AB
AB
ͬ��FM��DC����FM��![]() DC
DC
��AB��AC��DC��AC��
��AB��DC��EM��FM��
���1����2
��EM��AB��FM��DC��
���2����4����1����3��
���4����3
�ߡ�AGE+��4��180�㣬��GEC+��3��180�㣬
���AGE����GEC
���ı���AGEC�ǵ��ڽ��ı���
֤����������AE
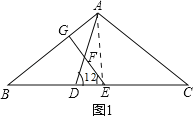
���B�Ķ���Ϊx
��AB��AC��CD��CA��
���C����B��x����1��![]() ��90�㩁
��90�㩁![]()
��F��AD���е㣬
��AF��EF��![]() AD��
AD��
���2����1��90�㩁![]()
���AGE����B+��2��x+90�㩁![]() ��90��+
��90��+![]() ����GEC��180�㩁��90�㩁
����GEC��180�㩁��90�㩁![]() ����90��+
����90��+![]()
���AGE����GEC��
���ı���AGEC�ǵ��ڽ��ı���
��3�����ڵ��ڽ��ı��Σ�Ϊ�ı���AGHC��
���ɣ���ͼ������AE��CF���ڵ�O��
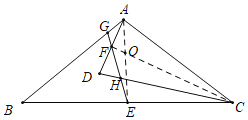
��CA��CD��AF��DF��
��CF��AD����ACF����DCF��
��AB��AC��BE��EC��
��AE��BC��
���AFC����AEC��90�㣬
��A��F��E��C�ĵ㹲Բ��
��AEF����ACF����OCH��
���FHC����HEC+��HCE����AEF+90��+��HCE����OCH+��HCE+90�㣽90��+��OCE��
�ߡ�AGF����B+��BEG����B+90�㩁��AEG��90��+��ACB����ACO��90��+��OCE��
���AGF����GHC��
���ı���AGHC�ǵ��ڽ��ı���