Question

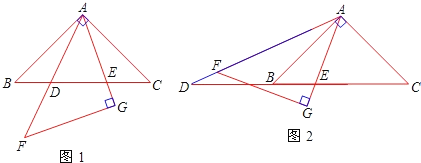
【题目】如图，在△ABC中，AB=BC，∠ABC=90°，D是AB上一动点，连接CD，以CD为直径的⊙M交AC于点E，连接BM并延长交AC于点F，交⊙M于点G,连接BE．

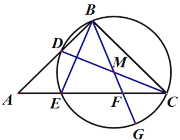
（1）求证：点B在⊙M上．

（2）当点D移动到使CD⊥BE时，求BC：BD的值．

（3）当点D到移动到使时，求证：AE+CF=EF．

Answer 1

【答案】（1）见解析；（2）BC：BD=；（3）见解析.

【解析】

（1）根据直角三角形斜边上的中线等于斜边的一半可得出BM=DM=CM，即可得证；

（2）连接DE，先证得BD=DE ，再证明AE=DE=DB，由勾股定理得到AD=，进一步得出BC=AB=，从而得解；

（3）连接EM,先证出△DME是等边三角形，得到AE=DE=EM，再证∠EMF=90°,再证出CF=MF，然后由勾股定理可得到EM+MF=EF，即AE+CF=EF.

（1）∵CD为⊙M的直径

∴CM=DM=CD

∵∠ABC=90°

∴BM=CM=DM=CD

∴点B在⊙M上

（2）如图，连接DE，

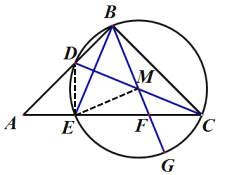
∵CD为⊙M的直径，CD⊥BE

∴∠DEC=90°, ,

∴∠DEA=90°, BD=DE ，

∵AB=BC，∠ABC=90°,

∴∠A=∠ACB=45° ,

∴∠ADE=180°-∠A-∠AED=45°,

∴∠ADE=∠A=45°,

∴AE=DE ,

∴AE=DE=DB,

∴AD= ,

∴AB=AD+BD=，

∴BC=AB=

∴BC：BD=

（3）如图，连接EM,

∵∠EMB=2∠ECB，由（2）知∠ECB=45°，

∴ ∠EMB=90°，

∴ ∠EMF=90°，

∴ EM+MF=EF ，

∵ ，

∴∠CMG=30°，

∴∠DME=60°，

∵DM=EM，

∴△DME是等边三角形.

∴DE=EM，∠CDE=60°，

由（2）知AE=DE，

∴AE=ME ，

∵∠AEC=90°， ∠CDE=60°，

∴∠DCE=30°，

∴∠DCE=∠CMG=30°

∴CF=MF，

∵ EM+MF=EF

∴ AE+CF=EF.