题目内容
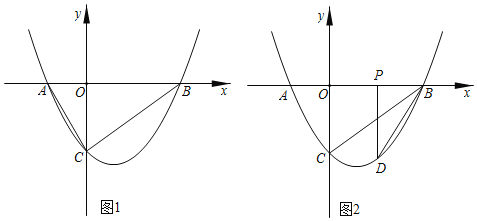
【题目】如图，点A、B分别在反比例函数y=
(k1＞0) 和 y=
(k2＜0)的图象上，连接AB交y轴于点P，且点A与点B关于P成中心对称.若△AOB的面积为4，则k1-k2=______.
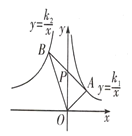
【答案】8
【解析】
作AC⊥y轴于C，BD⊥y轴于D，如图，先证明△ACP≌△BDP得到S△ACP=S△BDP，利用等量代换和k的几何意义得到=S△AOC+S△BOD=
×|k1|+|k2|=4，然后利用k1＜0，k2＞0可得到k2-k1的值．
解：
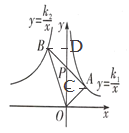
作AC⊥y轴于C，BD⊥y轴于D，如图，
∵点A与点B关于P成中心对称.
∴P点为AB的中点，
∴AP=BP，
在△ACP和△BDP中
，
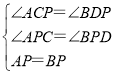∴△ACP≌△BDP（AAS），
∴S△ACP=S△BDP，
∴S△AOB=S△APO+S△BPO=S△AOC+S△BOD=×|k1|+|k2|=4，
∴|k1|+|k2|=8
∵k1＞0，k2＜0，
∴k1-k2=8．
故答案为8．
练习册系列答案
名校课堂系列答案
相关题目
【题目】4月23日，为迎接“世界读书日”，某书城开展购书有奖活动.顾客每购书满100元获得一次摸奖机会，规则为：一个不透明的袋子中装有4个小球，小球上分别标有数字1，2，3，4，它们除所标数字外完全相同，摇匀后同时从中随机摸出两个小球，则两球所标数字之和与奖励的购书券金额的对应关系如下：
两球所标数字之和 | 3 | 4 | 5 | 6 | 7 |
奖励的购书券金额（元） | 0 | 0 | 30 | 60 | 90 |
（1）通过列表或画树状图的方法计算摸奖一次获得90元购书券的概率；
（2）书城规定：如果顾客不愿意参加摸奖，那么可以直接获得30元的购书券.在“参加摸奖”和“直接获得购书券”两种方式中，你认为哪种方式对顾客更合算？请通过求平均教的方法说明理由.
