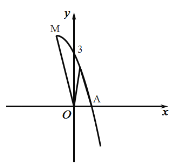��Ŀ����
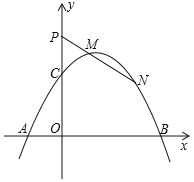
����Ŀ����֪������y��ax2��2ax+3��x�ύ�ڵ�A��B��A��B�ң�����AB��4����y�ύ��C�㣮
��1���������ߵĽ���ʽ��
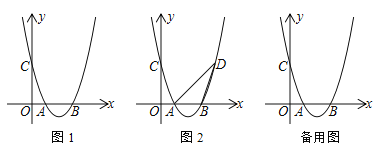
��2����ͼ��֤�����������������һ��P��0��b����b��3�������ڹ���P��һ��ֱ�߽���������M��N���㣬ʹ��PM��MN������
��3��������������0��x��4��IJ��ּ�Ϊͼ��G����ͼ��G��ֱ��y��t�Ϸ��IJ�����y��t���ۣ����ಿ�ֱ��ֲ��䣬�õ�һ���µĺ�����ͼ��������������ֵΪm����СֵΪn����m��n��6����t��ȡֵ��Χ��
���𰸡���1��y����x2+2x+3����2�������������3����2��t��1��
��������
��1��������y��ax2��2ax+3�ĶԳ���Ϊx��1����AB��4���ɶԳ��Ե�A����1��0����B��3��0����������⣻
��2��֤����PMG�ա�NMH��AAS����yG+yH��2yM��������⣻
��3���ֵ�D���ڵ�H��4��-5���Ϸ�����D���ڵ�H��4��-5���·�����������ֱ���⼴�ɣ�
�⣺��1��������y��ax2��2ax+3�ĶԳ���Ϊx��1����AB��4���ɶԳ��Ե�A��-1��0����B��3��0����
��A��-1��0������y��ax2��2ax+3����a+2a+3��0����a��-1��
�������ߵĽ���ʽΪy��-x2+2x+3��
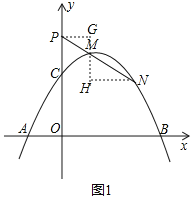
��2����ͼ����M��GH��x�ᣬPG��x�ᣬNH��x�ᣬ
��PM��MN�����PMG�ա�NMH��AAS����
��PG��NH��MG��MH��
��M��m��-m2+2m+3������N��2m��-4m2+4m+3����
��P��0��b����GM��MH��
��yG+yH��2yM��
��b+��-4m2+4m+3����2��-m2+2m+3������2m2��b-3��
��b��3��
�����m�ķ���������������ȵ�ʵ������
�˼�˵���˵�M��N���ڣ���ʹ��PM��MN��֤�ϣ�
��3��ͼ����ǰ������ͼ��ʾ���䶥��ֱ�ΪD��1��4����D����1��2t��4����
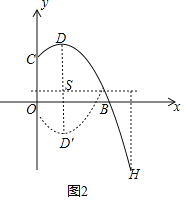
�ٵ�D���ڵ�H��4��-5���Ϸ�ʱ��
2t��4��-5����t��-![]() ��
��
��ʱ��m��t��n��-5����m-n��6����t+5��6����t��1��
��-![]() ��t��1��
��t��1��
�ڵ���D���ڵ�H��4��-5���·�ʱ��
ͬ���ɵã�t��-![]() ��m��t��n��2t-4��
��m��t��n��2t-4��
��m-n��6����t-��2t-4����6��
��t��-2����-2��t��-![]() ��
��
����������t��ȡֵ��ΧΪ����2��t��1��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��4��23�գ�Ϊӭ�����������������ij��ǿ�չ�����н��.�˿�ÿ������100Ԫ���һ���������ᣬ����Ϊ��һ�������Ĵ�����װ��4��С��С���Ϸֱ��������1��2��3��4�����dz�������������ȫ��ͬ��ҡ�Ⱥ�ͬʱ���������������С����������������֮���뽱���Ĺ���ȯ���Ķ�Ӧ��ϵ���£�
������������֮�� | 3 | 4 | 5 | 6 | 7 |
�����Ĺ���ȯ��Ԫ�� | 0 | 0 | 30 | 60 | 90 |
��1��ͨ���б�����״ͼ�ķ�����������һ�λ��90Ԫ����ȯ�ĸ��ʣ�
��2����ǹ涨������˿Ͳ�Ը��μ���������ô����ֱ�ӻ��30Ԫ�Ĺ���ȯ.�����μ�����������ֱ�ӻ�ù���ȯ�����ַ�ʽ�У�����Ϊ���ַ�ʽ�Թ˿����㣿��ͨ����ƽ���̵ķ���˵������.