Question

【题目】如图，在Rt△ABC中，∠A＝90°，∠ACB＝30°，AC＝10，CD是角平分线．

（1）如图1，若E是AC边上的一个定点，在CD上找一点P，使PA+PE的值最小；

（2）如图2，若E是AC边上的一个动点，在CD上找一点P，使PA+PE的值最小，并直接写出其最小值．

Answer 1

【答案】（1）点P位置见解析；（2）点P位置见解析，5.

【解析】

（1）如图，过D作DF⊥BC于F，过F作EF⊥AC交CD于P，于是得到结论；

（2）如图，过D作DF⊥BC于F，过F作EF⊥AC交CD于P，则此时，PA+PE的值最小；PA+PE的最小值=EF，根据角平分线的性质得到DA=DF，即点A与点F关于CD对称，根据直角三角形的性质即可得到结论．

（1）如图，

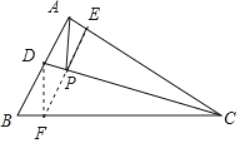
过D作DF⊥BC于F，过F作EF⊥AC交CD于P，

则此时，PA+PE的值最小；

点P即为所求；

（2）如图，过D作DF⊥BC于F，过F作EF⊥AC交CD于P，

则此时，PA+PE的值最小；

PA+PE的最小值＝EF，

∵CD是角平分线，∠BAC＝90°，

∴DA＝DF，

即点A与点F关于CD对称，

∴CF＝AC＝10，

∵∠ACB＝30°，

∴EF＝CF＝5．