��Ŀ����
����Ŀ���ҹ��Ŵ���ѧ������ֶ���λ������ǰ�У���������Ǿ���һ������ͼ����������εĹ��취�������ϵ�������1������ÿ������Ϊ���Ϸ���������֮�ͣ��������ˣ�a+b��n��nΪ����������չ��ʽ����a�Ĵ����������У���ϵ���������磬���������е�һ�е�������1��2��1��ǡ�ö�Ӧ��a+b��2��a2+2ab+b2չ��ʽ�е�ϵ���������е��ĸ���1��3��3��1��ǡ�ö�Ӧ�ţ�a+b��3��a3+3ab+3ab2+b3չ��ʽ�е�ϵ������϶�������ǵ����������������
��1����a+b��2չ��ʽa2+2ab+b2��ÿһ��Ĵ��������� ���Σ�
��a+b��3չ��ʽa3+3a2b+3ab2+b3��ÿһ��Ĵ��������� ���Σ�
��ô��a+b��nչ��ʽ��ÿһ��Ĵ��������� ���Σ�
��2��д����a+1��4��չ��ʽ�� ����
��3����չӦ�ã����㣨x+1��5+��x��1��6+��x+1��7�Ľ���У�x5���ϵ��Ϊ�� ����
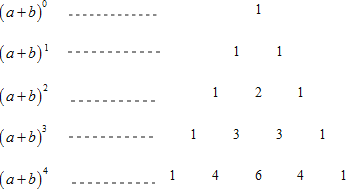
���𰸡���1��2��3��n����2��a4+4a3b+6a2b2+4ab3+b4��3��16.
��������
��1���۲죨a+b��2չ��ʽ�ͣ�a+b��3չ��ʽ�и�����ɵô𰸣��Ӷ��Ƴ���a+b��n��չ���
��2�������������ͼ�п�֪��a+1��4��չ��ʽ�ĸ���ϵ�������ɵý⣻
��3����x+1��5��x5���ϵ��Ϊ1���ٰ�������ǣ��ֱ���ã�x��1��6�ͣ�x+1��7չ��ʽ��x5���ϵ��������ϵ����Ӽ��ɵô𰸣�
�⣺��1����a+b��2չ��ʽa2+2ab+b2�е���ֱ�Ϊ��a2��2ab��b2�����ǵĴ�������2��
��a+b��3չ��ʽa3+3a2b+3ab2+b3�е���ֱ�Ϊ��a3��3a2b��3ab2��b3�����ǵĴ�������3��
�ɴ��Ƴ���a+b��nչ��ʽ�Ĵ�������n��
�ʴ�Ϊ��2��3��n��
��2�������������ͼ�п�֪��a+1��4��չ��ʽ�ĸ���ϵ���ֱ�Ϊ��1��4��6��4��1��չ��ʽΪ����a+1��4��a4+4a3b+6a2b2+4ab3+b4��
�ʴ�Ϊ��a4+4a3b+6a2b2+4ab3+b4��
��3����x+1��5��x5���ϵ��Ϊ1��
����������ǿ�֪��x��1��6��x6+6x5����1��+��+1����x+1��7��x7+7x6��1+21x5��12+��+1��
�ࣨx+1��5+��x��1��6+��x+1��7�Ľ���У�x5���ϵ��Ϊ��1+6������1��+21��16
�ʴ�Ϊ��16��