题目内容
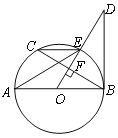
【题目】如图,在△OAB中,OA=OB,以点O为圆心的⊙O经过AB的中点C,直线AO与⊙O相交于点E、D,OB交⊙O于点F,P是![]() 的中点,连接CE、CF、BP.
的中点,连接CE、CF、BP.
(1)求证:AB是⊙O的切线.
(2)若OA=4,则
①当![]() 长为_____时,四边形OECF是菱形;
长为_____时,四边形OECF是菱形;
②当![]() 长为_____时,四边形OCBP是正方形.
长为_____时,四边形OCBP是正方形.![]()

【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)证明垂直就可以证明是切线.(2)利用四边形OECF是菱形的性质反推可得到DP长.利用正方形OECF的性质反推可得到DP长.
解:(1)∵在△ABO中,OA=OB,C是AB的中点,
∴OC⊥AB.
∵OC为⊙O的半径,
∴AB是⊙O的切线.
(2)①∵OECF为菱形,
∴OE=EC,∠EOC=∠COF.
∴OE=EC=OC.
∴∠EOC=∠COF=60°.
∴∠DOF=60°.
又∵P为弧DF的中点,
∴∠DOP=30°.
∵∠AOC=60°,∠OCA=90°,
∴OC=![]() OA=2.
OA=2.
∴弧DP的长=![]() .
.
②∵四边形OCBP为正方形,
∴∠COB=∠POB=45°.
∴OC=![]() OB=2
OB=2![]() .
.
∵P为弧DF的中点,
∴∠DOP=45°.
∴弧DP的长=![]() .
.
故答案为:①![]() ;②
;②![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】(1)某校招聘教师一名,现有甲、乙、丙三人通过专业知识、讲课、答辩三项测试,他们各自的成绩如下表所示:
应聘者 | 专业知识 | 讲课 | 答辩 |
甲 | 70 | 85 | 80 |
乙 | 90 | 85 | 75 |
丙 | 80 | 90 | 85 |
按照招聘简章要求,对专业知识、讲课、答辩三项赋权5:4:1.请计算三名应聘者的平均成绩,从成绩看,应该录取谁?
(2)我市举行了某学科实验操作考试,有A、B、C、D四个实验,规定每位学生只参加其中一个实验的考试,并由学生自己抽签决定具体的考试实验.小王,小张,小厉都参加了本次考试.
①小厉参加实验D考试的概率是 ;
②用列表或画树状图的方法求小王、小张抽到同一个实验的概率.