Question

【题目】如图，已知抛物线与轴交于、两点，与轴交于点．

（1）求抛物线的解析式；

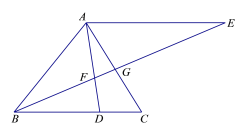
（2）点是第一象限内抛物线上的一个动点（与点、不重合），过点作轴于点，交直线于点，连接、．设点的横坐标为，的面积为．求关于的函数解析式及自变量的取值范围，并求出的最大值；

（3）已知为抛物线对称轴上一动点，若是以为直角边的直角三角形，请直接写出点的坐标．

Answer 1

【答案】（1）；（2），当时，有最大值，最大值；（3），

【解析】

（1）由抛物线与x轴的两个交点坐标可设抛物线的解析式为y=a（x+1）（x-3），将点C（0，3）代入抛物线解析式中即可得出关于a一元一次方程，解方程即可求出a的值，从而得出抛物线的解析式；

（2）设直线BC的函数解析式为y=kx+b．结合点B、点C的坐标利用待定系数法求出直线BC的函数解析式，再由点D横坐标为m找出点D、点E的坐标，结合两点间的距离公式以及三角形的面积公式求出函数解析式，利用配方法将S关于m的函数关系式进行变形，从而得出结论；

（3）先求出对称轴，设M(1，y)，然后分分BM为斜边和CM为斜边两种情况求解即可；

解：（1）∵抛物线与x轴交于A（-1，0）、B（3，0）两点，

∴设抛物线的解析式为y=a（x+1）（x-3），

又∵点C（0，3）在抛物线图象上，

∴3=a×（0+1）×（0-3），解得：a=-1．

∴抛物线解析式为y=-（x+1）（x-3）=-x2+2x+3．

∴抛物线解析式为；

（2）设直线的函数解析式为，

∵直线过点，，

∴，解得，

∴，

设，，

∴，

∴，

∵，

∴当时，有最大值，最大值；

（3）∵，

∴对称轴为直线x=1，

设M(1，y)，

则CM2=1+(y-3)2=y2-6y+10，

BM2=y2+(1-3)2=y2+4，

BC2=9+9=18.

当BM为斜边时，

则y2-6y+10+18= y2+4，

解得

y=4，

此时M(1,4)；

当CM为斜边时，

y2+4+18= y2-6y+10，

解得

y=-2，

此时M(1，-2)；

综上可得点的坐标为，.