��Ŀ����
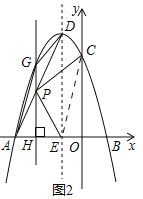
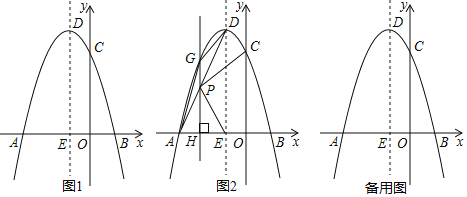
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y����x2+bx+c��x��ֱ���A����3��0����B���㣬��y�ύ�ڵ�C����DΪ�����ߵĶ��㣬�����ߵĶԳ�����x����1������x�ύ��E�㣮
��1����ֱ��д�������ߵĽ���ʽ������D�����ꣻ
��2����ͼ2������AD�����P���߶�AD�ϵ�һ�����㣬����P��x��Ĵ��߽��������ڵ�G����x���ڵ�H������AG��GD������ADG�����Ϊ1ʱ��
�����P�����ꣻ
������PC��PE��̽��PC��PE��������ϵ��λ�ù�ϵ����˵������;
��3����MΪ��������һ���㣬NΪ�����ߵĶԳ�����һ���㣬QΪx����һ���㣬����Q��M��N��EΪ������ı���Ϊ������ʱ����ֱ��д����Q�����꣮
���𰸡���1��y����x2��2x+3������D����Ϊ����1��4������2����P����2��2������PC��PE��PC��PE�����ɼ���������3��Q��![]() ��0����
��0����![]() ��0����
��0����![]() ��0����
��0����![]() ��0��
��0��
��������
��1�����ݴ���ϵ���������ɵõ��𰸣�
��2��������ֱ��AD�Ľ���ʽΪ��y��2x+6�����P��m��2m+6������3��m����1������G��m����m2��2m+3�����õ�PG=��m2��4m��3�����S��ADG��1���г�����m�ķ��̼��ɣ�
������CE�����ݹ��ɶ����ֱ����PC��PE�� CE��ֵ�����ɵõ�PC��PE��������ϵ��λ�ù�ϵ��
��3����N����1��n����Q��p��0������������ã�M��p��n����|p+1|��|n|����p2��2p+3��n�����������Q������.
��1����������y����x2+bx+c�ĶԳ�����x����1��
�ੁ![]() ����1��
����1��
��b����2��
��������y����x2+bx+c�Ľ���ʽΪy����x2��2x+c��
�������߹���A����3��0����
��0����9+6+c��
��c��3��
�������ߵĽ���ʽΪy����x2��2x+3��
�ඥ��D����Ϊ����1��4����
��2�����ɣ�1��֪��D����1��4����
��A����3��0����
��ֱ��AD�Ľ���ʽΪ��y��2x+6��
���P��m��2m+6������3��m����1����
�ɣ�1��֪�������ߵĽ���ʽΪ��y����x2��2x+3��
��PH��x�ᣬ
��G��m����m2��2m+3����
��PG����m2��2m+3����2m+6������m2��4m��3��
�ߡ�ADG�����Ϊ1��
��S��ADG��![]() PG������1+3������m2��4m��3��1��
PG������1+3������m2��4m��3��1��
��m����2��
��P����2��2����
����ͼ2������CE���ɣ�1��֪�������ߵĽ���ʽΪy����x2��2x+3��
��C��0��3����
�ɢ�֪��P����2��2����
�������ߵĶԳ���x��1��
��E����1��0����
��PC��![]() ��PE��
��PE��![]() ��
��![]() �� CE��
�� CE��![]() ��
��
��PC��PE��PC2+PE2��5+5��10��CE2��
���PCE����CEΪб�ߵ�ֱ�������Σ�
���CPE��90����
��PC��PE��
��3����N����1��n����Q��p��0����
����Q��M��N��EΪ������ı���Ϊ�����Σ�
��M��p��n����|p+1|��|n|�٣�
�ߵ�M���������ϣ�
�ੁp2��2p+3��n�ڣ�
�����٢ڽ�ã�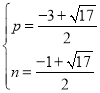 ��
��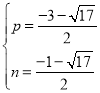 ��
��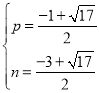 ��
��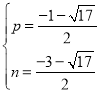 ��
��
��Q��![]() ��0����
��0����![]() ��0����
��0����![]() ��0����
��0����![]() ��0����
��0����