Question

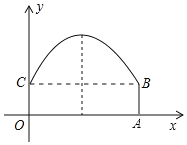
【题目】如图是数值转换机的示意图，小明按照其对应关系画出了y与x的函数图象（如图）：

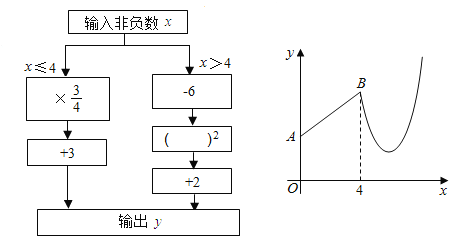
（1）分别写出当0≤x≤4与x＞4时，y与x的函数关系式：

（2）求出所输出的y的值中最小一个数值；

（3）写出当x满足什么范围时，输出的y的值满足3≤y≤6．

Answer 1

【答案】（1）当时，y=x+3； 当时 y=(x-6)2+2

（2）最小值2 （3） 0≤x≤5或7≤x≤8

【解析】

（1）当0≤x≤4时，函数关系式为y=x+3；当x＞4时，函数关系式为y=（x﹣6）2+2；

（2）根据一次函数与二次函数的性质，分别求出自变量在其取值范围内的最小值，然后比较即可；

（3）由题意，可得不等式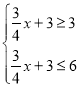和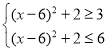，解答出x的值即可．

解：（1）由图可知，

当0≤x≤4时，y=x+3；

当x＞4时，y=（x﹣6）2+2；

（2）当0≤x≤4时，y=x+3，此时y随x的增大而增大，

∴当x=0时，y=x+3有最小值，为y=3；

当x＞4时，y=（x﹣6）2+2，y在顶点处取最小值，

即当x=6时，y=（x﹣6）2+2的最小值为y=2；

∴所输出的y的值中最小一个数值为2；

（3）由题意得，当0≤x≤4时，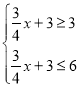

解得，0≤x≤4；

当x＞4时，

，

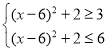解得，4≤x≤5或7≤x≤8；

综上，x的取值范围是：0≤x≤5或7≤x≤8．