题目内容
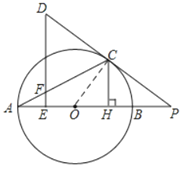
【题目】如图,AB为⊙O直径,AC为⊙O的弦,过⊙O外的点D作DE⊥OA于点E,交AC于点F,连接DC并延长交AB的延长线于点P,且∠D=2∠A,作CH⊥AB于点H.
(1)判断直线DC与⊙O的位置关系,并说明理由;
(2)若HB=2,cosD=![]() ,请求出AC的长.
,请求出AC的长.

【答案】(1)DC与⊙O相切;(2)![]() .
.
【解析】试题分析:(1)连接OC,易证∠COB=∠D,由于∠P+∠D=90°,所以∠P+∠COB=90°,从而可知半径OC⊥DC;
(2)由(1)可知:cos∠COP=cos∠D=![]() ,设半径为r,所以OH=r﹣2,从而可求出r的值,利用勾股定理即可求出CH的长度,从而可求出AC的长度.
,设半径为r,所以OH=r﹣2,从而可求出r的值,利用勾股定理即可求出CH的长度,从而可求出AC的长度.
试题解析:解:(1)DC与⊙O相切.理由如下:
连接OC,∵∠COB=2∠A,∠D=2∠A,∴∠COB=∠D,∵DE⊥AP,∴∠DEP=90°,在Rt△DEP中,∠DEP=90°,∴∠P+∠D=90°,∴∠P+∠COB=90°,∴∠OCP=90°,∴半径OC⊥DC,∴DC与⊙O相切.
(2)由(1)可知:∠OCP=90°,∠COP=∠D,∴cos∠COP=cos∠D=![]() ,∵CH⊥OP,∴∠CHO=90°,设⊙O的半径为r,则OH=r﹣2.在Rt△CHO中,cos∠HOC=
,∵CH⊥OP,∴∠CHO=90°,设⊙O的半径为r,则OH=r﹣2.在Rt△CHO中,cos∠HOC=![]() =
=![]() =
=![]() ,∴r=5,∴OH=5﹣2=3,∴由勾股定理可知:CH=4,∴AH=AB﹣HB=10﹣2=8.
,∴r=5,∴OH=5﹣2=3,∴由勾股定理可知:CH=4,∴AH=AB﹣HB=10﹣2=8.
在Rt△AHC中,∠CHA=90°,∴由勾股定理可知:AC=![]() .
.

练习册系列答案
相关题目