��Ŀ����
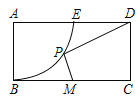
����Ŀ����ͼһ����֪������y��ax2+bx+c��ͼ����A��0��3����B��1��0������Գ���Ϊֱ��l��x��2������A��AC��x�ύ�������ڵ�C����AOB��ƽ���߽��߶�AC�ڵ�E����P���������ϵ�һ�����㣬���������Ϊm��
��1���������ߵĽ���ʽ��
��2��������P��ֱ��OE�·����������ϣ�����PE��PO����mΪ��ֵʱ���ı���AOPE��������������ֵ�����ı���AOPE������ʱ�����߶�OE��ȡ��M����y����ȡ��N����PM+MN+![]() ANȡ��Сֵʱ�������ʱN������꣮
ANȡ��Сֵʱ�������ʱN������꣮
��3����ͼ����F�������ߵĶԳ���l�ϵ�һ�㣬�����������Ƿ���ڵ�P��ʹ��POF��Ϊ�Ե�PΪֱ�Ƕ���ĵ���ֱ�������Σ������ڣ�ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y��x2��4x+3����2��N��0��![]() ������3�����ڣ����ɣ�������.
������3�����ڣ����ɣ�������.
��������
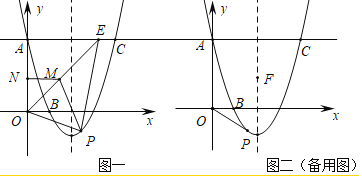
��1������������x�����һ������ΪD���ɶԳ��Եã�D��3��0�����������ߵĽ���ʽΪ��y=a��x-1����x-3������A��0��3������ã�3=3a��a=1��������⣻
��2������A����б��Ϊ45����ֱ��AH������P��PH��AH�ڵ�H����OE�ڵ�M����y���ڵ�N�����NΪ��������⣻
��3����P�ڶԳ������ߣ�����x���·���P�ڶԳ������ߣ�����x���Ϸ���P�ڶԳ�����ұߣ�����x���·���P�ڶԳ�����ұߣ�����x���Ϸ�����������ֱ���⼴�ɣ�
�⣺��1������������x�����һ������ΪD��
�ɶԳ��Եã�D��3��0����
�������ߵĽ���ʽΪ��y��a��x��1����x��3����
��A��0��3������ã�3��3a��a��1��
�������ߵĽ���ʽ��y��x2��4x+3��
��2����ͼ1���ߡ�AOE������Ƕ�ֵ�����Ե���OEP������ʱ���ı���AOPE������
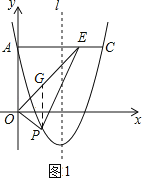
��P��m��m2��4m+3����
��OEƽ�֡�AOB����AOB��90�㣬���AOE��45�㣬���AOE�ǵ���ֱ�������Σ�
��AE��OA��3����E��3��3������OE�Ľ���ʽΪ��y��x��
��P��PG��y�ᣬ��OE�ڵ�G����G��m��m����
��PG��m����m2��4m+3������m2+5m��3��
��S�ı���AOPE��S��AOE+S��POE��![]() ��3��3+
��3��3+![]() PGAE��
PGAE��![]() +
+![]() ��3������m2+5m��3������
��3������m2+5m��3������![]() m2+
m2+![]() ��
��
�ߩ�![]() ��0��
��0��
�൱m��![]() ʱ��S�����ֵ����ʱ��P��
ʱ��S�����ֵ����ʱ��P��![]() ����
����![]() ����
����
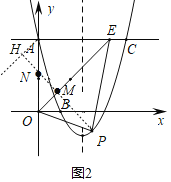
����A����б��Ϊ45���ֱ��AH������P��PH��AH�ڵ�H����OE�ڵ�M����y���ڵ�N�����NΪ����
��NH��![]() AN��
AN��
��ʱPM+MN+![]() AN��PM+MN+HN��PHΪ��Сֵ��
AN��PM+MN+HN��PHΪ��Сֵ��
��ֱ��PH�ı���ʽΪ��y����x+b������P�����������ʽ����ã�
ֱ��PH�ı���ʽΪ��y����x+![]() ��
��
�ʵ�N��0��![]() ����
����
��3�����ڣ����ɣ�
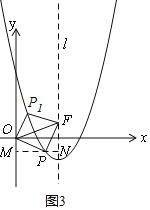
�ٵ�P�ڶԳ������ߣ�����x���·�ʱ����ͼ2����P��MN��y�ᣬ��y����M����l��N��
�ߡ�OPF�ǵ���ֱ�������Σ���OP��PF��
���OMP�ա�PNF��AAS����
��OM��PN��
��P��m��m2��4m+3������m2+4m��3��2��m��
��ã�m��![]() ����ȥ����
����ȥ����![]()
��P��������![]() ��
��![]() ����
����
�ڵ�P�ڶԳ������ߣ�����x���Ϸ�ʱ����ͼ3��
ͬ���ã�2��m��m2��4m+3����ã�m��![]() ��
��![]() ����ȥ����
����ȥ����
�ʵ�P��![]() ��
��![]() ����
����
�۵�P�ڶԳ�����ұߣ�����x���·�ʱ��
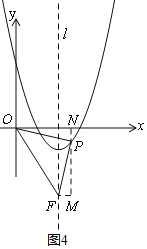
��ͼ3����P��MN��x����N����F��FM��MN��M��
ͬ���á�ONP�ա�PMF��
��PN��FM��
��m2+4m��3��m��2��
��ã�m��![]() ��
��![]() ����ȥ����
����ȥ����
P��������![]() ��
��![]() ����
����
�ܵ�P�ڶԳ�����ұߣ�����x���Ϸ�ʱ��
ͬ����m2��4m+3��m��2��
��ã�m��![]() ��
��![]() ����ȥ����
����ȥ����
��P����������![]() ��
��![]() ����
����
���ϣ���P������Ϊ����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����

 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д�