题目内容
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
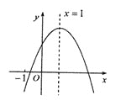
①abc>0;②b>a+c;③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
【答案】B
【解析】根据抛物线的开口方向、x=-1、x=3时的函数值小于0、对称轴x=-![]() =1及函数的最大值逐一判断可得.
=1及函数的最大值逐一判断可得.
∵抛物线开口向下,
∴a<0,
∵-![]() >0,
>0,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,
∴结论①错误;
∵当x=-1时,y=a-b+c<0,即b>a+c,
∴结论②正确;
∵当x=-1和x=3时,函数值相等,均小于0,
∴y=9a+3b+c<0,
∴结论③错误;
∵x=-![]() =1,
=1,
∴b=-2a,
由x=-1时,y=a-b+c<0得a+2a+c<0,即c<-3a,
∴④正确;
由图象知当x=1时函数取得最大值,
∴am2+bm+c≤a+b+c,即a+b≥m(am+b),
故⑤正确;
故选:B.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a,b的值.