题目内容
【题目】如图,已知等边△ABC的边长为8,E是边AC中点,点D、P分别在边AB、BC上(BP<PC),且BD=3.∠DPE=60°.求BP的长.
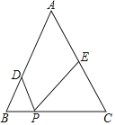
【答案】BP=2
【解析】
根据等边三角形的性质易得∠B=∠C,然后利用三角形外角性质可得∠DPC=∠B+∠BDP=∠DPE+∠EPC,进而推出∠BDP=∠EPC,即可判定△BDP∽△CPE,再由对应边成比例,建立方程求出BP.
解: ∵△ABC是等边三角形,
∴AB=BC=AC=8,∠B=∠C=60°,
∵E是边AC中点,
∴CE=4,
∵∠DPC=∠B+∠BDP=∠DPE+∠EPC,且∠DPE=60°,
∴∠BDP=∠EPC,且∠B=∠C,
∴△BDP∽△CPE,
∴![]() ,
,
∴3×4=BP(8﹣BP)
解得BP=2或6,
∵BP<PC,
∴BP=2.

练习册系列答案
相关题目