题目内容
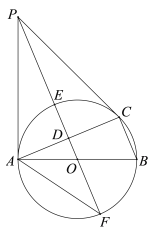
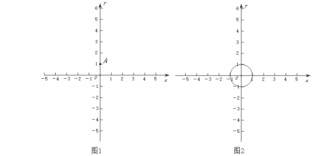
【题目】如图1,矩形ABCD的对角线AC与BD相交于点O,将矩形沿对角线AC折叠,折叠后点B落在点E处,CE交AD于点F,连接DE.
(1)求证:![]() ;
;
(2)当AB与BC满足什么数量关系时,四边形AODE是菱形?请说明理由;
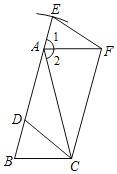
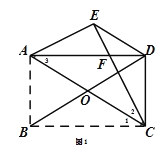
(3)将图1中的矩形ABCD改为平行四边形ABCD,其它条件不变,如图2,若AB=![]() ,∠ABC=30°,点E在直线AD上方,试探究:△AED是直角三角形时,BC的长度是多少.
,∠ABC=30°,点E在直线AD上方,试探究:△AED是直角三角形时,BC的长度是多少.

【答案】(1)证明见解析;(2)当![]() 时,四边形ABCD是菱形,理由见解析;(3)BC=12或8.
时,四边形ABCD是菱形,理由见解析;(3)BC=12或8.
【解析】
(1)根据折叠的性质和平行线的判定定理,即可解答;
(2)先利用折叠的性质,证明四边形AODE是平行四边形,再利用菱形的判定定理即可解答;
(3)根据折叠的性质,再分两种情况进行讨论即可解答.
(1)∵矩形ABCD沿AC折叠
∴∠1=∠2
∵AD∥BC
∴∠1=∠3
∴∠2=∠3
∴AF=CF
∵AD=BC,BC=CE,
∴AD=CE,
∴AD-AF=CE-CF
即EF=DF,
∴∠FED=∠FDE
∵∠AFC=∠EFD,
∴∠3=∠ADE,
∴AC∥DE
(2)当![]() 时,四边形ABCD是菱形.
时,四边形ABCD是菱形.
理由如下:∵在Rt△ABC中,![]()
∴∠1=30°
∴∠3=∠1=30°,∠BAO=60°
∵矩形ABCD沿AC折叠
∴∠BAO=∠CAE=60°
在矩形ABCD中,OA=DO
∴∠3=∠ADO=30°
∴∠EAD=∠CAE-∠3=30°
∴∠EAD=∠ADO
∴AE∥OD
由(1)可知AC∥DE,
∴四边形AODE是平行四边形
又∵OA=DO,
∴四边形AODE是菱形
(3)∵沿AC折叠,
∴∠ACB=∠ACE,BC=CE
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠DAC=∠ACE,
∴FA=FC
∵AD=BC,BC=CE,
∴AD=CE,
∴AD-FA=CE-FC
即EF=DF
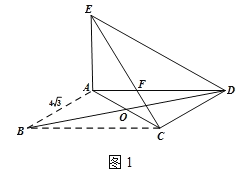
①![]() 时,如图1,依题可知
时,如图1,依题可知
![]() ,
,![]()
在![]() 中,
中,![]()
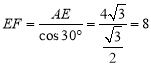 ,
,
∴![]() ,
,
∴![]() .
.
②如图2,当![]() 时,
时,
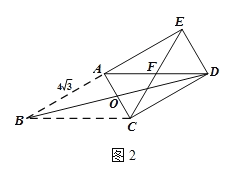
∵∠AEC=∠ABC=30°,
∴∠FED=60°
∵EF=FD,
∴∠FDE=∠FED=60°
在Rt△AED中,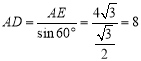 ,
,
∴![]()
综上可知:当点E在直线AD上方时,BC=12或8.

 阅读快车系列答案
阅读快车系列答案