Question

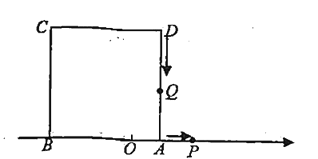
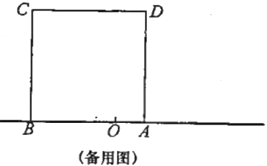
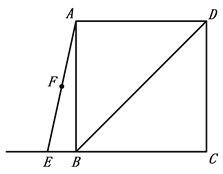
【题目】如图，在正方形ABCD中，连接BD，点E为CB边的延长线上一点，点F是线段AE的中点，过点F作AE的垂线交BD于点M,连接ME、MC.

（1）根据题意补全图形，猜想与的数量关系并证明；

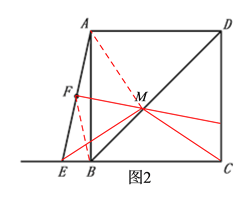
（2）连接FB，判断FB 、FM之间的数量关系并证明.

Answer 1

【答案】（1）=（2）

【解析】

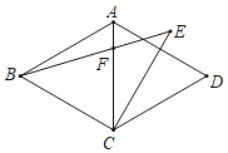
（1）①按照题中要求补全图形即可；②如图1，连接AM，由已知条件易得MF是AE的垂直平分线，由此可得MA=ME，由四边形ABCD是正方形易得点A和点C关于BD对称，由此可得MA=MC，从而可得ME=MC，进而可得∠MEC=∠MCE；

（2）如图2，由已知易得∠MAD=∠MCD结合∠MEC=∠MCE可得∠MAD+∠MEC=∠MCD+∠MCE=90°，由AD∥CB可得∠MAD+∠MEC+∠MAE+∠MEA=180°，由此可得∠MAE+∠MEA=90°，从而可得∠AME=90°，结合点F是AE的中点可得MF=AE，结合在Rt△ABE中，BF=AE即可得到BF=MF.

（1）①按题要求补全图形如下图所示：

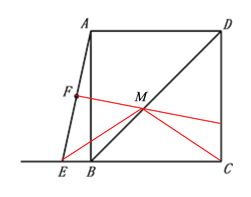
②∠MEC=∠MCE，理由如下：

如图1，连接AM，

∵点F是AE的中点，FM⊥AE，

∴MA=ME，

∵点A、点C是关于正方形ABCD对角线BD所在直线的对称点，

∴MA=MC，

∴ME=MC，

∴∠MEC=∠MCE；

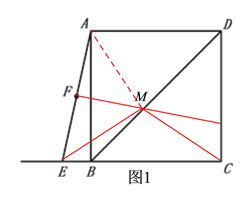
（2）如图2，FB=FM，理由如下：

∵点M在正方形ABCD的对角线BD，

∴，

∴=，

∵=，

∴ ，

∵ ，

∴ ，

∴，

∴，

∵ 点F是AE的中点，

∴

∵ 在△ABE中，∠ABE=90°，点F是AE的中点，

∴ ，

∴ .