题目内容
【题目】综合题
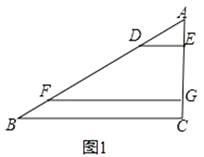
(1)如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= , ![]() = .
= . 
(2)如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.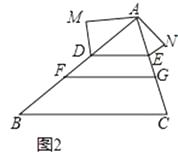
【答案】
(1)2,2
(2)证明:∵DE∥FG∥BC,
∴ ![]() ,
,
∵AM=BF,MD=DF,AN=GC,NE=EG,
∴ ![]() ,
,
∴△ADM∽△AEN,
∴∠M=∠N
【解析】(1)解:∵DE∥FG,
∴ ![]() ,
,
∵AD=2,AE=1,DF=4,
∴EG=2,
∴AF=AD+DF=6,AG=AE+EG=3,
∵DE∥FG∥BC,
∴ ![]() =2;
=2;
故答案为:2,2;
(1)根据平行线分线段成比例定理得出:AD∶DF=AE∶EG ,从而得出EG的长,进而得出AF,AG的长 ,再根据平行线分线段成比例定理得出FB∶GC=AF∶AG ,从而得出答案;
(2)根据平行线分线段成比例定理得出:AD∶AE=DF∶EG=FB∶GC ,又AM=BF,MD=DF,AN=GC,根据等量代换得出AD∶AE=MD∶NE=AM∶AN ,从而判断出△ADM∽△AEN,根据相似三角形对应角相等得出结论。

练习册系列答案
相关题目