题目内容
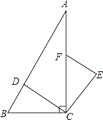
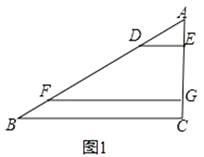
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1 , 此时AP1= ![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+
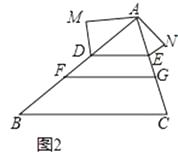
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=1+ ![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ![]() ;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= .
;…,按此规律继续旋转,直至得到点P2015为止.则AP2015= . 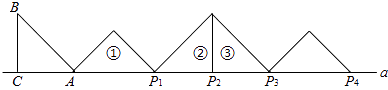
【答案】1343+672 ![]()
【解析】解:AP1= ![]() ,AP2=1+
,AP2=1+ ![]() ,AP3=2+
,AP3=2+ ![]() ;
;
AP4=2+2 ![]() ;AP5=3+2
;AP5=3+2 ![]() ;AP6=4+2
;AP6=4+2 ![]() ;
;
AP7=4+3 ![]() ;AP8=5+3
;AP8=5+3 ![]() ;AP9=6+3
;AP9=6+3 ![]() ;
;
∵2015=3×671+2,
∴AP2013=(2013﹣671)+671 ![]() =1342+671
=1342+671 ![]() ,
,
∴AP2014=1342+671 ![]() +
+ ![]() =1342+672
=1342+672 ![]() ,
,
∴AP2015=1342+672 ![]() +1=1343+672
+1=1343+672 ![]() .
.
所以答案是:1343+672 ![]() .
.
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= ![]() 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 . 
【题目】为了“让所有的孩子都能上得起来,都能上好学”,国家自2007年起出台了一系列“资助贫困学生”的政策,其中包括向经济困难的学生免费提供教科书的政策.为确保这项工作顺利实施,学校需要调查学生的家庭情况.以下是某市城郊一所中学甲、乙两个班的调查结果,整理成表(一)和图(一):
| 城镇户口 (非低保) | 农村户口 | 城镇低保 | 总人数 |
甲班/人 | 20 | 5 |
| |
乙班/人 | 28 | 22 | 4 |
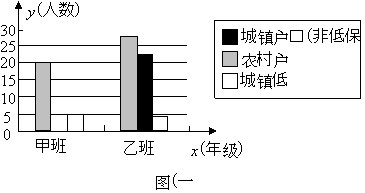
(1)将表(一)和图(一)中的空缺部分补全;
(2)现要预定2009年下学期的教科书,全额100元.若农村户口学生可全免,城镇低保的学生可减免![]() 城镇户口(非低保)学生全额交费.求乙班应交书费多少元?甲班受到国家资助教科书的学生占全班人数的百分比是多少?
城镇户口(非低保)学生全额交费.求乙班应交书费多少元?甲班受到国家资助教科书的学生占全班人数的百分比是多少?
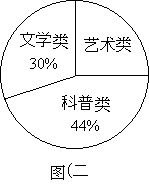
(3)五四青年节时,校团委免费赠送给甲、乙两班若干册科普类、文学类及艺术类三种图书,其中文学类图书有15册,三种图书所占比例如图(二)所示,求艺术类图书共有多少册?