题目内容
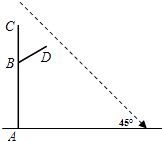
【题目】如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)求证:AE∥CF.
(2)BC平分∠DBE吗?为什么?

【答案】(1)见详解;(2)BC平分∠DBE,证明见详解.
【解析】
(1)根据同角的补角相等,证明∠2=∠DBE,问题得证;
(2)先证明AD∥BC,进而证明∠C=∠CBD,再根据AE∥CF,证明∠CBD=∠CBE,问题得证.
解:(1)证明:∵∠1+∠2=180°,∠1+∠DBE=180°,
∴∠2=∠DBE,
∴AE∥CF;
(2)BC平分∠DBE,
证明:∵AE∥CF,
∴∠C+∠CBA=180°,
∵∠A=∠C,
∴∠A+∠CBA=180°,
∴AD∥BC,
∴∠ADB=∠CBD,∠FDA=∠C,
∵DA平分∠BDF,
∴∠FDA=∠ADB,
∴∠C=∠CBD,
∵AE∥CF,
∴∠C=∠CBE,
∴∠CBD=∠CBE,
∴BC平分∠DBE.

练习册系列答案
相关题目