题目内容
【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
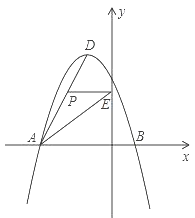
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
【答案】(1) y=-x2-2x+3;(-1,4);(2)S=-x2-3x(-3<x<-1),S最大值![]() .(3)P′(
.(3)P′(![]() ,
,![]() ).点P′不在该抛物线上.
).点P′不在该抛物线上.
【解析】
试题分析:(1)由抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,则代入求得a,b,c,进而得解析式与顶点D.
(2)由P在AD上,则可求AD解析式表示P点.由S△APE=![]() PEyP,所以S可表示,进而由函数最值性质易得S最值.
PEyP,所以S可表示,进而由函数最值性质易得S最值.
(3)由最值时,P为(-![]() ,3),则E与C重合.画示意图,P'过作P'M⊥y轴,设边长通过解直角三角形可求各边长度,进而得P'坐标.判断P′是否在该抛物线上,将xP'坐标代入解析式,判断是否为yP'即可.
,3),则E与C重合.画示意图,P'过作P'M⊥y轴,设边长通过解直角三角形可求各边长度,进而得P'坐标.判断P′是否在该抛物线上,将xP'坐标代入解析式,判断是否为yP'即可.
试题解析:(1)∵抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,
∴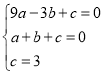 ,
,
解得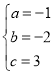 ,
,
∴解析式为y=-x2-2x+3
∵-x2-2x+3=-(x+1)2+4,
∴抛物线顶点坐标D为(-1,4).
(2)∵A(-3,0),D(-1,4),
∴设AD为解析式为y=kx+b,有![]() ,
,
解得![]() ,
,
∴AD解析式:y=2x+6,
∵P在AD上,
∴P(x,2x+6),
∴S△APE=![]() PEyP=
PEyP=![]() (-x)(2x+6)=-x2-3x(-3<x<-1),当x=-
(-x)(2x+6)=-x2-3x(-3<x<-1),当x=-![]() 时,S取最大值
时,S取最大值![]() .
.
(3)如图1,设P′F与y轴交于点N,过P′作P′M⊥y轴于点M,
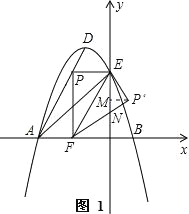
∵△PEF沿EF翻折得△P′EF,且P(-![]() ,3),
,3),
∴∠PFE=∠P′FE,PF=P′F=3,PE=P′E=![]() ,
,
∵PF∥y轴,
∴∠PFE=∠FEN,
∵∠PFE=∠P′FE,
∴∠FEN=∠P′FE,
∴EN=FN,
设EN=m,则FN=m,P′N=3-m.
在Rt△P′EN中,
∵(3-m)2+(![]() )2=m2,
)2=m2,
∴m=![]() .
.
∵S△P′EN=![]() P′NP′E=
P′NP′E=![]() ENP′M,
ENP′M,
∴P′M=![]() .
.
在Rt△EMP′中,
∵EM=![]() ,
,
∴OM=EO-EM=![]() ,
,
∴P′(![]() ,
,![]() ).
).
当x=![]() 时,y=-(
时,y=-(![]() )2-2
)2-2![]() +3=
+3=![]() ≠
≠![]() ,
,
∴点P′不在该抛物线上.