题目内容
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E交DC于点N.
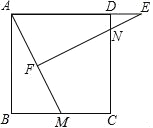
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
【答案】(1)证明见解析;(2)4.9.
【解析】
试题分析:(1)由正方形的性质得出AB=AD,∠B=90°,AD∥BC,得出∠AMB=∠EAF,再由∠B=∠AFE,即可得出结论;
(2)由勾股定理求出AM,得出AF,由△ABM∽△EFA得出比例式,求出AE,即可得出DE的长.
试题解析:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)解:∵∠B=90°,AB=12,BM=5,
∴AM=![]() =13,AD=12,
=13,AD=12,
∵F是AM的中点,
∴AF=![]() AM=6.5,
AM=6.5,
∵△ABM∽△EFA,
∴![]() ,
,
即![]() ,
,
∴AE=16.9,
∴DE=AE-AD=4.9.

练习册系列答案
相关题目