题目内容
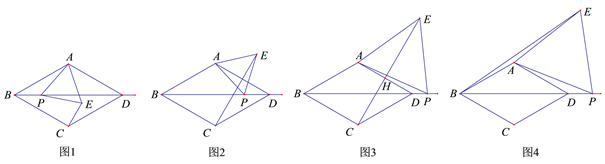
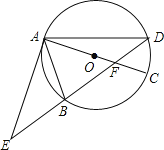
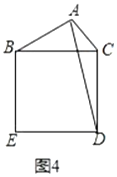
【题目】在菱形ABCD和菱形BEFG中,点A、B、G共线,点C在BE上,∠DAB=60°,AG=8,点M,N分别是AC和EG的中点,则MN的最小值等于( )
A.2![]() B.4C.2
B.4C.2![]() D.6
D.6
【答案】A
【解析】
连接BD、BF,延长AC交GE于H,连接BH,证明四边形BNHM是矩形,得出MN=BH,由直角三角形的性质得出GH,AH的长,当BH⊥AG时,BH最小,由直角三角形的性质得出BH的长,即可得出答案.
连接BD、BF,延长AC交GE于H,连接BH,如图所示:
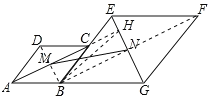
∵四边形ABCD和四边形BEFG是菱形,∠DAB=60°,∴AD∥BC∥GF,AC⊥BD,BF⊥GE,BE=BG,AM=CM,EN=GN,∴∠GAH=30°,∠EBG=∠DAB=60°,∴△BEG是等边三角形,∴∠BGE=60°,∴∠AHG=90°,∴四边形BNHM是矩形,GH![]() AG=4,AH
AG=4,AH![]() GH=4
GH=4![]() ,∴MN=BH,当BH⊥AG时,BH最小.
,∴MN=BH,当BH⊥AG时,BH最小.
∵∠GAH=30°,∴BH![]() AH=2
AH=2![]() ,∴MN的最小值=2
,∴MN的最小值=2![]() .
.
故选A.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目