ЬтФПФкШн
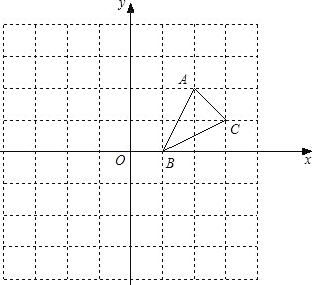
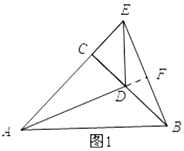
ЁОЬтФПЁПШчЭМ1ЃЌНЋСНИіЕШбќШ§НЧаЮ![]() КЭ
КЭ![]() ЦДКЯдквЛЦ№ЃЌЦфжа
ЦДКЯдквЛЦ№ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
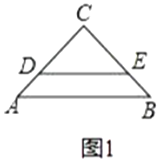
ЃЈ1ЃЉВйзїЗЂЯж
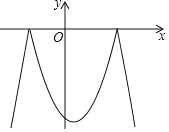
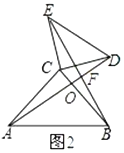
ШчЭМ2ЃЌЙЬЖЈ![]() ЃЌАб
ЃЌАб![]() ШЦзХЖЅЕу
ШЦзХЖЅЕу![]() а§зЊЃЌЪЙЕу
а§зЊЃЌЪЙЕу![]() Тфдк
Тфдк![]() БпЩЯ.
БпЩЯ.
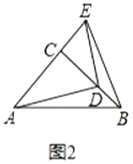
ЬюПеЃКЯпЖЮ![]() гы
гы![]() ЕФЙиЯЕЪЧЂйЮЛжУЙиЯЕЃК______ЃЛЂкЪ§СПЙиЯЕЃК______
ЕФЙиЯЕЪЧЂйЮЛжУЙиЯЕЃК______ЃЛЂкЪ§СПЙиЯЕЃК______
ЃЈ2ЃЉБфЪНЬНОП
ЕБ![]() ШЦЕу
ШЦЕу![]() а§зЊЕНЭМ3ЕФЮЛжУЪБЃЌЃЈ1ЃЉжаЕФНсТлЛЙГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЛ
а§зЊЕНЭМ3ЕФЮЛжУЪБЃЌЃЈ1ЃЉжаЕФНсТлЛЙГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЛ
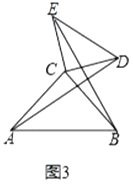
ЃЈ3ЃЉНтОіЮЪЬт
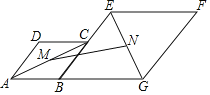
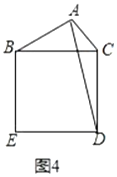
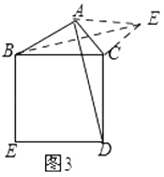
ШчЭМ4ЃЌвбжЊЯпЖЮ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЃЌвд
ЃЌвд![]() ЮЊБпзївЛИіе§ЗНаЮ
ЮЊБпзївЛИіе§ЗНаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЫцзХБп
ЃЌЫцзХБп![]() ЕФБфЛЏЃЌЯпЖЮ
ЕФБфЛЏЃЌЯпЖЮ![]() ЕФГЄвВЛсЗЂЩњБфЛЏ.ЧыжБНгаДГіЯпЖЮ
ЕФГЄвВЛсЗЂЩњБфЛЏ.ЧыжБНгаДГіЯпЖЮ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЌЂк
ЃЌЂк![]() ЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .вРОн
.вРОн![]() жЄУї
жЄУї![]() ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУЕН
ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУЕН![]() ЃЌШЛКѓдйгЩ
ЃЌШЛКѓдйгЩ![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУЕН
ЃЌПЩЕУЕН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЫљЪОЃКМЧ![]() гы
гы![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() .ЯШжЄУї
.ЯШжЄУї![]() ЃЌШЛКѓвРОн
ЃЌШЛКѓвРОн![]() жЄУї
жЄУї![]() ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУЕН
ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУЕН![]() ЃЌШЛКѓгЩ
ЃЌШЛКѓгЩ![]() ЃЌ
ЃЌ![]() ЃЌПЩжЄУї
ЃЌПЩжЄУї![]() ЃЛ
ЃЛ
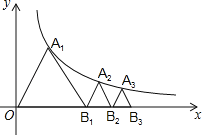
ЃЈ3ЃЉЙ§Еу![]() зї
зї![]() ЃЌШЁ
ЃЌШЁ![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌЯШдкЕШбќжБНЧ
ЃЌЯШдкЕШбќжБНЧ![]() жаЧѓЕУ
жаЧѓЕУ![]() ЕФГЄЃЌШЛКѓвРОнШ§НЧаЮЕФШ§БпЙиЯЕПЩЧѓЕУ
ЕФГЄЃЌШЛКѓвРОнШ§НЧаЮЕФШ§БпЙиЯЕПЩЧѓЕУ![]() ЕФШЁжЕЗЖЮЇЃЌзюКѓвРОн
ЕФШЁжЕЗЖЮЇЃЌзюКѓвРОн![]() жЄУї
жЄУї![]() ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪЕУЕН
ЃЌгЩШЋЕШШ§НЧаЮЕФаджЪЕУЕН![]() ЃЌЙЪДЫПЩЧѓЕУ
ЃЌЙЪДЫПЩЧѓЕУ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
НтЃКЃЈ1ЃЉбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() .
.
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ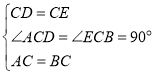 ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() ЃЌ
ЃЌ![]() .
.
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() .
.
ЙЪД№АИЮЊЃК![]() ЃЌ
ЃЌ![]() .
.
ЃЈ2ЃЉШчЭМ2ЫљЪОЃКМЧ![]() гы
гы![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФНЛЕуЮЊ
ЕФНЛЕуЮЊ![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() .
.
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ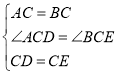 ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() ЃЌ
ЃЌ![]() .
.
гжЁп![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() .
.
ЃЈ3ЃЉШчЭМ3ЫљЪОЃКЙ§Еу![]() зї
зї![]() ЃЌШЁ
ЃЌШЁ![]() ЃЌСЌНс
ЃЌСЌНс![]() .
.
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() .
.
дк![]() КЭ
КЭ![]() жа
жа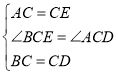 ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() .
.
Ёр![]() .
.

 УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ
УПШе10ЗжжгПкЫуаФЫуЫйЫуЬьЬьСЗЯЕСаД№АИ