题目内容
【题目】如图,⊙O为等边△ABC的外接圆,其半径为1,P为弧AB上的动点(P点不与A、B重合),连接AP,BP,CP.
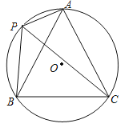
(1)求证:PA+PB=PC.
(2)求四边形APBC面积的最大值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)在PC上截取PD=AP,利用圆周角定理得到∠APC=60°,则△APD是等边三角形,根据等边三角形的性质得到AD=AP=PD,∠ADP=60°,进而推出∠ADC=∠APB,即可证明△APB≌△ADC,利用对应边相等即可得证;
(2)过点P作PE⊥AB于E,过点C作CF⊥AB于F,利用面积公式可得S四边形APBC=![]() AB(PE+CF),易知PC为⊙O的直径时,四边形APBC的面积最大,求出三角形ABC的边长即可求面积.
AB(PE+CF),易知PC为⊙O的直径时,四边形APBC的面积最大,求出三角形ABC的边长即可求面积.
解:在PC上截取PD=AP,如图1,

∵△ABC为等边三角形,
∴∠ABC=∠BAC=60°,
∴∠APC=∠ABC=60°,
又∵PD=AP
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=∠APC+∠BAC =120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
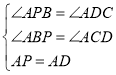 ,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴PC=PD+DC=PA+PB;
(2)当点P为弧AB的中点时,四边形APBC的面积最大.
理由如下,如图2,过点P作PE⊥AB,垂足为E.
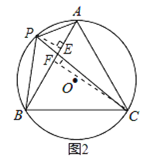
过点C作CF⊥AB,垂足为F.
∵S△APB=![]() ABPE,S△ABC=
ABPE,S△ABC=![]() ABCF,
ABCF,
∴S四边形APBC=![]() AB(PE+CF),
AB(PE+CF),
当点P为弧AB的中点时,PE+CF=PC,PC为⊙O的直径,
∴此时四边形APBC的面积最大.
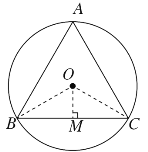
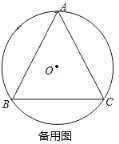
如图所示,过O作OM⊥BC,连接OB,OC,
∵⊙O为等边△ABC的外接圆,
∴∠BOC=120°,
由垂径定理可知∠BOM=60°,BM=MC=![]() BC,
BC,
∴![]()
∴![]()
∴其内接正三角形的边长AB=![]() ,
,
∴S四边形APBC=![]() ×2×
×2×![]() .
.

【题目】某射击队教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
(1)根据上述信息可知:甲命中环数的中位数是_____环,乙命中环数的众数是______环;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会变小.(填“变大”、“变小”或“不变”)