��Ŀ����
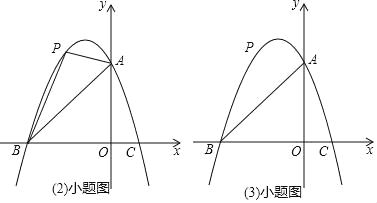
����Ŀ����֪����ͼ��������y��ax2+bx+3��������ֱ��ڵ�A��B����3��0����C��1��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮
��1���������߽���ʽ��
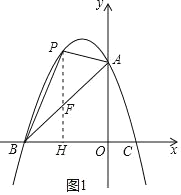
��2������P�˶���ʲôλ��ʱ����PAB��������
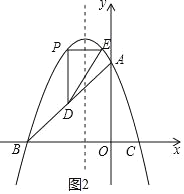
��3������P��x��Ĵ��ߣ����߶�AB�ڵ�D���ٹ���P��PE��x�ύ�������ڵ�E������DE�������Ƿ���ڵ�Pʹ��PDEΪ����ֱ�������Σ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1��y����x2��2x+3 ��2������![]() ��
��![]() �� ��3�����ڣ�P����2��3����P��
�� ��3�����ڣ�P����2��3����P��![]() ��
��![]() ��
��
��������
��1���ô���ϵ������⣻��2������P��PH��x���ڵ�H����AB�ڵ�F��ֱ��AB����ʽΪy��x+3����P��t����t2��2t+3������3��t��0������F��t��t+3������PF����t2��2t+3����t+3������t2��3t������S��PAB��S��PAF+S��PBFд������ʽ�����������ֵ����3����P��t����t2��2t+3������3��t��0������D��t��t+3����PD����t2��3t����������y����x2��2x+3������x+1��2+4���ɶԳ���Ϊֱ��x����1��PE��x�ύ�������ڵ�E����yE��yP������E��P���ڶԳ���Գƣ�����![]() ����1����xE����2��xP����2��t����PE��|xE��xP|��|��2��2t|���ɡ�PDEΪ����ֱ�������Σ���DPE��90�㣬��PD��PE���ٷ�������ۣ��ٵ���3��t�ܩ�1ʱ��PE����2��2t���ڵ���1��t��0ʱ��PE��2+2t
����1����xE����2��xP����2��t����PE��|xE��xP|��|��2��2t|���ɡ�PDEΪ����ֱ�������Σ���DPE��90�㣬��PD��PE���ٷ�������ۣ��ٵ���3��t�ܩ�1ʱ��PE����2��2t���ڵ���1��t��0ʱ��PE��2+2t
�⣺��1����������y��ax2+bx+3����B����3��0����C��1��0��
��![]() ��ã�
��ã�![]()
�������߽���ʽΪy����x2��2x+3
��2������P��PH��x���ڵ�H����AB�ڵ�F
��x��0ʱ��y����x2��2x+3��3
��A��0��3��
��ֱ��AB����ʽΪy��x+3
�ߵ�P���߶�AB�Ϸ���������
����P��t����t2��2t+3������3��t��0��
��F��t��t+3��
��PF����t2��2t+3����t+3������t2��3t
��S��PAB��S��PAF+S��PBF��![]() PFOH+
PFOH+![]() PFBH��
PFBH��![]() PFOB��
PFOB��![]() ����t2��3t������
����t2��3t������![]() ��t+
��t+![]() ��2+
��2+![]()
���P�˶�������Ϊ����![]() ��
��![]() ������PAB������
������PAB������
��3�����ڵ�Pʹ��PDEΪ����ֱ��������
��P��t����t2��2t+3������3��t��0������D��t��t+3��
��PD����t2��2t+3����t+3������t2��3t
��������y����x2��2x+3������x+1��2+4
��Գ���Ϊֱ��x����1
��PE��x�ύ�������ڵ�E
��yE��yP������E��P���ڶԳ���Գ�
��![]() ����1
����1
��xE����2��xP����2��t
��PE��|xE��xP|��|��2��2t|
�ߡ�PDEΪ����ֱ�������Σ���DPE��90��
��PD��PE
�ٵ���3��t�ܩ�1ʱ��PE����2��2t
�ੁt2��3t����2��2t
��ã�t1��1����ȥ����t2����2
��P����2��3��
�ڵ���1��t��0ʱ��PE��2+2t
�ੁt2��3t��2+2t
��ã�t1��![]() ��t2��
��t2��![]() ����ȥ��
����ȥ��
��P��![]() ��
��![]() ��
��
������������P��������2��3����![]() ��
��![]() ��ʱʹ��PDEΪ����ֱ�������Σ�
��ʱʹ��PDEΪ����ֱ�������Σ�

 ��У����ϵ�д�
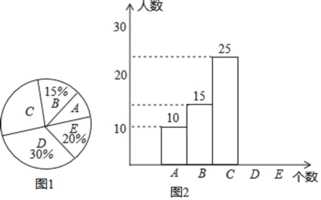
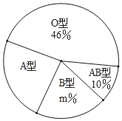
��У����ϵ�д�����Ŀ����ֻҪ�����׳�һ�㰮�����罫������õ��˼䡱��ij��ѧ���á�������Ѫ�ա���չ��Ը������Ѫ���������⣬��Ѫ��Ѫ���С�A��B��AB��O���������ͣ������ȡ������Ѫ�������ͳ�ƣ����ݽ����������ͼ����������ͳ��ͼ��������ͼ����
Ѫ��ͳ�Ʊ�
Ѫ�� | A | B | AB | O |
���� | �� �� | 10 | 5 | �� �� |
��1�����������ȡ��Ѫ������Ϊ�� ���ˣ�ͼ��m���� ����
��2����ȫ���е����ݣ�
��3������λ�и�У��1300��������Ѫ�����ƴ�Լ�ж�������A��Ѫ��
��4������4����Ը��Ѫ�ߣ�2��ΪO�ͣ�1��ΪA�ͣ�1��ΪB�ͣ�����4���������ѡ2�ˣ�������״ͼ���б���������Ѫ�;�ΪO�͵ĸ��ʣ�
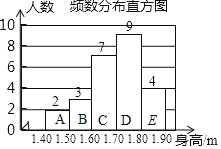
����Ŀ��ijУ������������д��������ÿλѧ����д����39�������������������鲿��ѧ����д�����ͼ1��ͼ2�Ǹ��ݳ�������Ƶ�ͳ��ͼ��һ���֣�
��� | ��д��ȷ�ĸ���x | ���� |
A | 0��x��8 | 10 |
B | 8��x��16 | 15 |
C | 16��x��24 | 25 |
D | 24��x��32 | m |
E | 32��x��40 | n |
����������Ϣ����������⣺
��1�����ι��������˶�����ѧ�������m��n��ֵ����ȫͼ2������ͳ��ͼ��
��2�����ͼ1�С����Ķ�����
��3����У����3000��ѧ���������д��ȷ�ĸ�������24����Ϊ���ϸ������������ѧУ���α�����д���ϸ��ѧ��������