题目内容
如图，在等腰△ABC中，AC=BC=10，以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC于F，交CB的延长线于点E．
（1）求证：直线EF是⊙O的切线；
（2）若sin∠E=
，求AB的长．
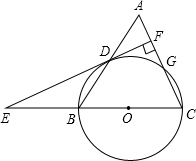
（1）求证：直线EF是⊙O的切线；
（2）若sin∠E=
| 2 |
| 5 |
（1）证明：连接OD，
∵AC=BC，
∴∠ABC=∠BAC，
∵OD=OB，
∴∠ABC=∠ODB，
∴∠BAC=∠BDO，
∴OD∥AC，
∵DF⊥AC，
∴OD⊥DF，
∵OD为半径，
∴直线EF是⊙O的切线；
（2）
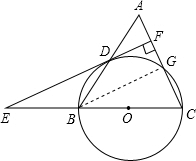连接BG，
∵BC是⊙O直径，
∴∠BGC=90°，
∵DF⊥AC，
∴∠DFC=90°=∠BGC，
∴BG∥EF，
∴∠E=∠GBC，
∵sin∠E=
，
∴sin∠GBC=
=
，
∵BC=10，
∴CG=4，
∴AG=10-4=6，由勾股定理得：BG=
=2
，
在Rt△BGA中，由勾股定理得：AB=
=
=2
，即AB=2
．
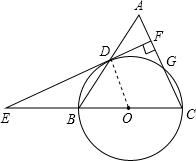
∵AC=BC，
∴∠ABC=∠BAC，
∵OD=OB，
∴∠ABC=∠ODB，
∴∠BAC=∠BDO，
∴OD∥AC，
∵DF⊥AC，
∴OD⊥DF，
∵OD为半径，
∴直线EF是⊙O的切线；
（2）
连接BG，∵BC是⊙O直径，
∴∠BGC=90°，
∵DF⊥AC，
∴∠DFC=90°=∠BGC，
∴BG∥EF，
∴∠E=∠GBC，
∵sin∠E=
| 2 |
| 5 |
∴sin∠GBC=
| 2 |
| 5 |
| CG |
| BC |
∵BC=10，
∴CG=4，
∴AG=10-4=6，由勾股定理得：BG=
| BC2-CG2 |
| 21 |
在Rt△BGA中，由勾股定理得：AB=
| BG2+AG2 |
(2
|
| 30 |
| 30 |
练习册系列答案
相关题目
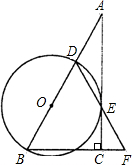
，与CA的延长线相交于点E，G是AD的中点，连接CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．
