题目内容
已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C
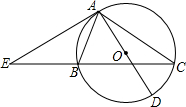
（1）如图①，若AB=1，∠P=30°，求AP的长（结果保留根号）；
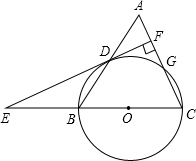
（2）如图②，若D为AP的中点，求证：直线CD是⊙O的切线．
（1）如图①，若AB=1，∠P=30°，求AP的长（结果保留根号）；
（2）如图②，若D为AP的中点，求证：直线CD是⊙O的切线．
（1）∵AB是⊙O的直径，AP是⊙O的切线，
∴BA⊥PA，
∴∠BAP=90°，
∵AB=1，∠P=30°，
∴AP=
AB=
；
（2）证明：连结OC、AC，如图，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴△ACP为直角三角形，
∵D为AP的中点，
∴DC=DA，
∴∠DCA=∠DAC，
∵OC=OA，
∴∠OCA=∠OAC，
∴∠OCA+∠DAC=∠OAC+∠DAC，
即∠OCD=∠OAD=90°，
∴OC⊥DC，
∴直线CD是⊙O的切线．
∴BA⊥PA，
∴∠BAP=90°，
∵AB=1，∠P=30°，
∴AP=
| 3 |
| 3 |
（2）证明：连结OC、AC，如图，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴△ACP为直角三角形，
∵D为AP的中点，
∴DC=DA，
∴∠DCA=∠DAC，
∵OC=OA，
∴∠OCA=∠OAC，
∴∠OCA+∠DAC=∠OAC+∠DAC，
即∠OCD=∠OAD=90°，
∴OC⊥DC，
∴直线CD是⊙O的切线．
练习册系列答案
相关题目
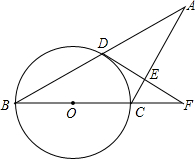交BC的延长线于点F．