题目内容
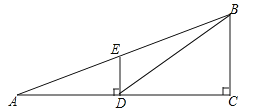
【题目】如图,在△ABC中,AB=AC,AD是BC边上的高,AM是△ABC外角∠CAE的平分线. 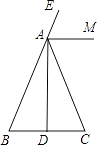
(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状,并证明你的结论.
【答案】
(1)解:如图所示:
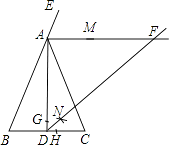
(2)解:△ADF是等腰直角三角形.
理由:∵AB=AC,AD是高,
∴∠BAD=∠CAD
又∵AM是△ABC外角∠CAE的平分线,
∴∠FAD= ![]() ×180°=90°,
×180°=90°,
∴AF∥BC,
∴∠CDF=∠AFD.
又∵∠AFD=∠ADF,
∴∠CDF=∠ADF.
∴AD=AF.
∴△ADF是等腰直角三角形
【解析】(1)以D为圆心,以任意长为半径画弧,交AD于G,交DC于H,分别以G、H为圆心,以大于 ![]() GH为半径画弧,两弧交于N,作射线DN,交AM于F.(2)求出∠BAD=∠CAD,求出∠FAD=
GH为半径画弧,两弧交于N,作射线DN,交AM于F.(2)求出∠BAD=∠CAD,求出∠FAD= ![]() ×180°=90°,求出∠CDF=∠AFD=∠ADF,推出AD=AF,即可得出答案.
×180°=90°,求出∠CDF=∠AFD=∠ADF,推出AD=AF,即可得出答案.
【考点精析】根据题目的已知条件,利用等腰直角三角形的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目